LeetCode刷题笔记-749. 隔离病毒-模拟+搜索
原文地址 zhuanlan.zhihu.com
题目描述
749. 隔离病毒 困难
病毒扩散得很快,现在你的任务是尽可能地通过安装防火墙来隔离病毒。
假设世界由 m x n 的二维矩阵 isInfected 组成, isInfected[i][j] == 0 表示该区域未感染病毒,而 isInfected[i][j] == 1 表示该区域已感染病毒。可以在任意 2 个相邻单元之间的共享边界上安装一个防火墙(并且只有一个防火墙)。
每天晚上,病毒会从被感染区域向相邻未感染区域扩散,除非被防火墙隔离。现由于资源有限,每天你只能安装一系列防火墙来隔离其中一个被病毒感染的区域(一个区域或连续的一片区域),且该感染区域对未感染区域的威胁最大且 保证唯一 。
你需要努力使得最后有部分区域不被病毒感染,如果可以成功,那么返回需要使用的防火墙个数; 如果无法实现,则返回在世界被病毒全部感染时已安装的防火墙个数。
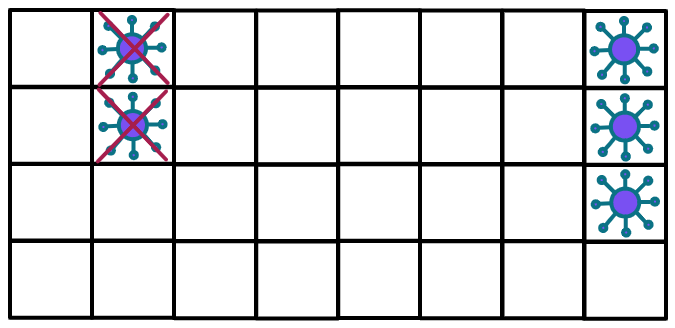
示例 1:
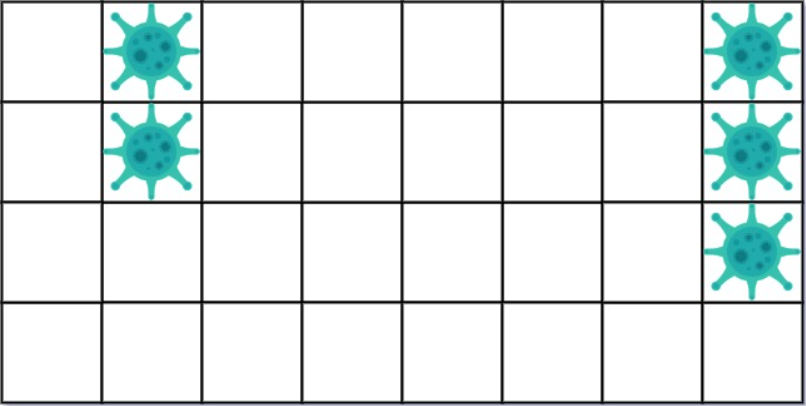
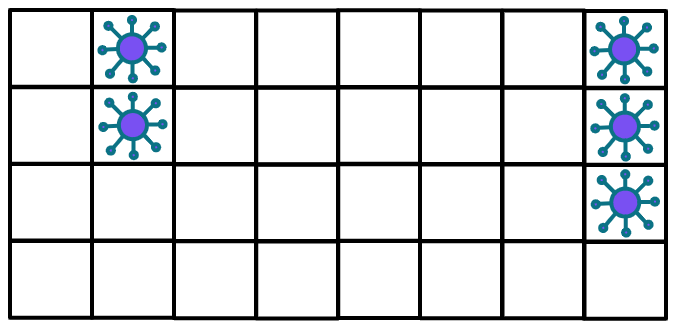
1 | 输入: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]] |
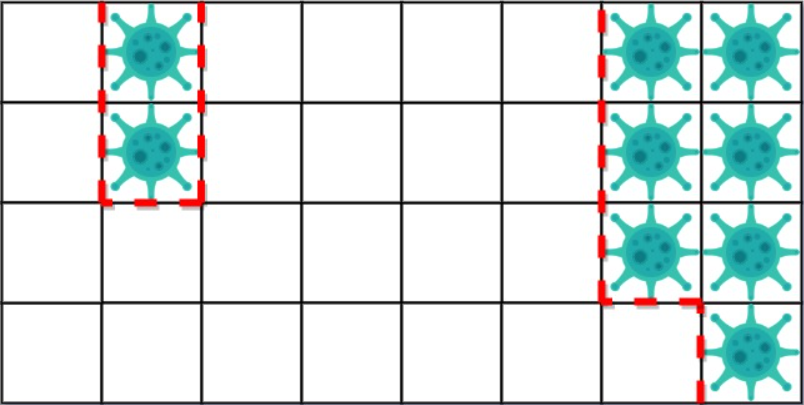
示例 2:
1 | 输入: isInfected = [[1,1,1],[1,0,1],[1,1,1]] |
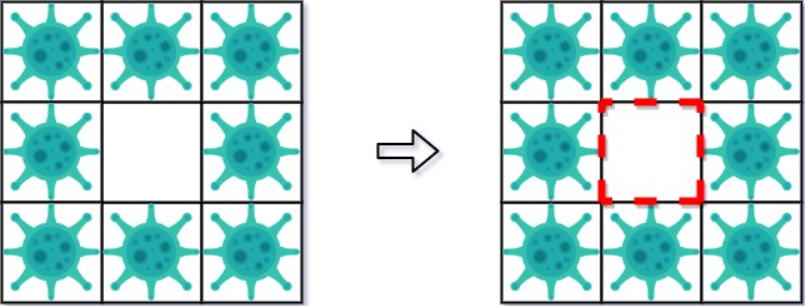
示例 3:
1 | 输入: isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]] |
解题思路
1 | NoYes获取当天最大的感染面积区域和所需的防火墙数目对最大感染面积区域的病毒进行阻断消杀存活的病毒进行扩散处理所需防火墙数目是否为零?输出结果 |
- 获取最大的感染面积区域和所需的防火墙数目
- 对最大感染面积区域的病毒进行阻断消杀
- 存活的病毒进行扩散处理
- 重复上述步骤,直到所需防火墙为 0 为止
如何获取最大感染面积
先遍历到病毒区域
对对每个病毒区域进行搜索
统计该区域可以感染的面积
统计该区域所需的防火墙
对当天最大病毒感染面积区域的病毒进行阻断消杀
对剩余病毒区域进行扩散处理
其中状态数s需要特别注意,因为每一天一个位置可以有四个方向来感染,同时也可以有多个病毒区域来感染。因此要进行区分,这里就是通过状态数s来完成的。


1 | func getMaxAreaNeedWalls() int { |
如何进行阻断消杀
- 对该病毒区域的病毒进行死亡标记
grid[x][y] = -2 - 对病毒位置进行四个方向的 DFS 搜索,同时需要做访问标记。
1 | func toDead(x, y int) { |
如何进行扩散处理
- 对当前病毒地点的四处进行 DFS 搜索。
- 如果为空,进行感染(边界条件)。
- 如果为病毒,继续搜索(状态转移)。

1 | func spread(x, y int, vis [][]int) { |
如何对病毒区域搜索
- 对当前病毒地点的四处进行 DFS 搜索。
- 如果为空,防火墙数
cur(函数内的全局变量)自增,且未访问过的话感染面积自增(边界条件)。 - 如果为病毒,继续搜索(状态转移)。

1 | func DFS(x, y, s int, vis [][]int) int { |
AC 代码(Go 语言)
1 | // 方向数组 |
用栈解决迷宫问题-Go语言
原文地址 zhuanlan.zhihu.com
用栈解决迷宫问题-Go语言
问题描述
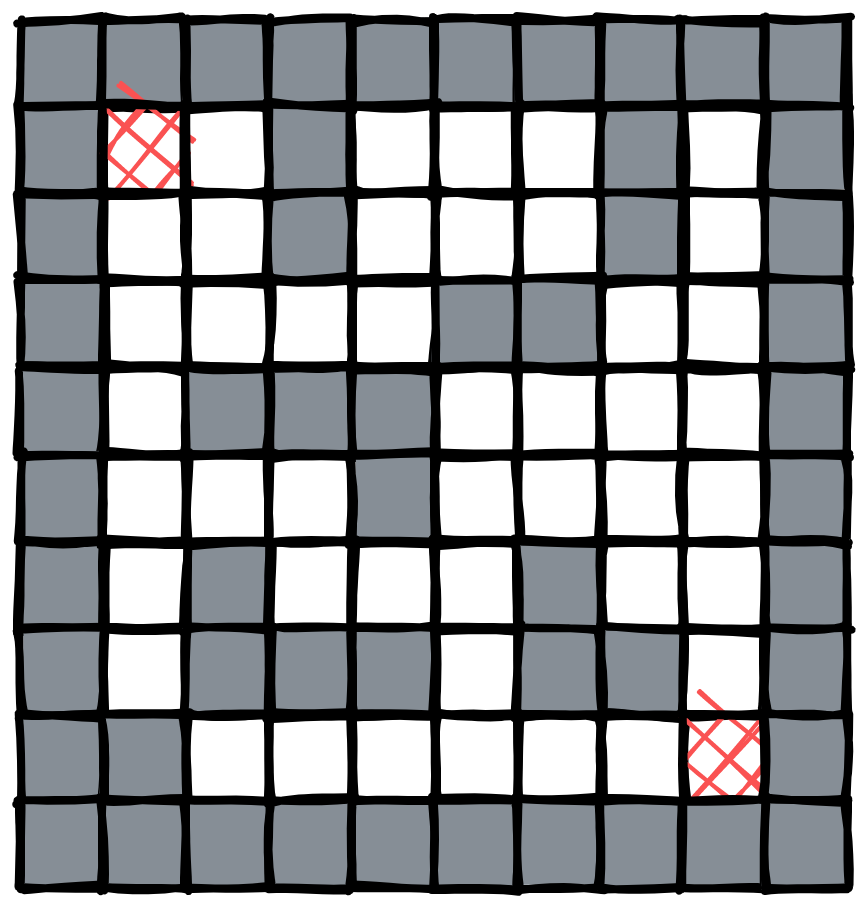
以上是一个迷宫,我们要从右上角的入口走到左下角的出口。现在要设计一个程序输出可走的路线,如果无法到达出口则输出不能。
问题分析
对于以上的迷宫图我们要用一个二维数组进行模拟:
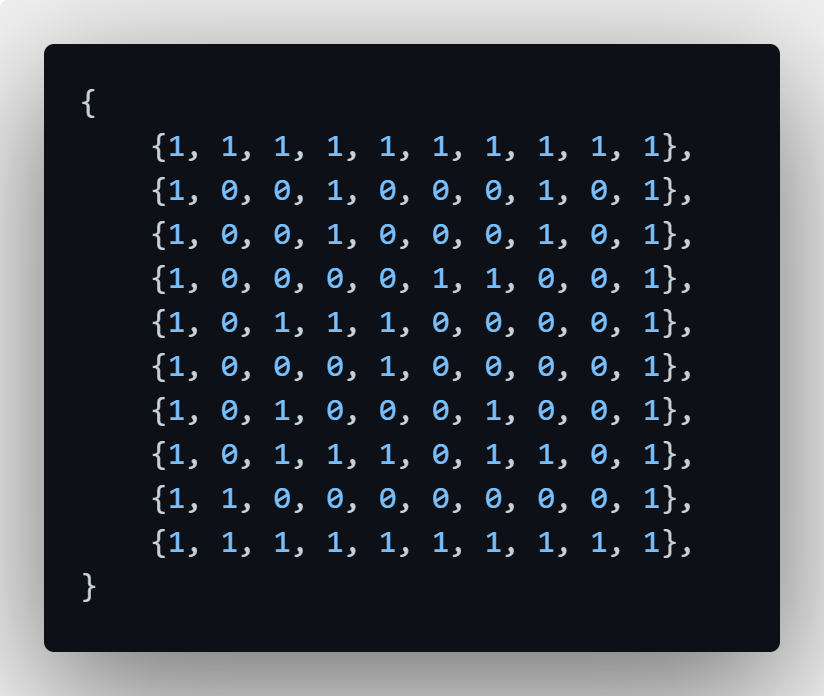
1 | const N, M = 8, 8 // 迷宫大小 |
首先要声明一个位置向量结构体:
1 | type pos struct { |
这里如果不存放指向dir的话我们很难知道当前位置点的哪些方向都遍历过了。
然后我们要针对这种位置向量设计一个栈:
1 | // 位置向量栈 |
迷宫的路径搜索
graph TD
A(创建路径栈和相关临时变量) --> B[初始位置向量入栈,并标记标记地图] -->C
C{判断是否为空栈} -->|No|I{是否到达终点}
I -->|Yes| K(输出路线)
I -->|No| D[朝四个方向依次进行遍历]
D --> E{是否找到可走路线} -->|Yes| F[记录可走方向,该可走的位置向量入栈]
E -->|No|G[无路可走,所以当前栈顶位置向量出栈并撤回标记]
F --> C
G --> C
C ----->|Yes| H(该迷宫行不通)
1 | // 迷宫路径搜索 |
完整代码
1 | package main |

一道高数极限计算题-泰勒展开法暴力求解
原文地址 zhuanlan.zhihu.com
$$
\lim_{x \to + \infty} x^2[(1 + \frac{1}{x + 1})^{x + 1} - (1 + \frac{1}{x})^x]
$$
解:
$$
= \lim_{x \to +\infty} x^2 [e^{(x + 1)\ln{(1 + \frac{1}{x + 1})}} - e^{x\ln{(1 + \frac{1}{x})}}]
$$
$$
泰勒公式 : ln(1 + x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \dots
$$
$$
其中 \lim_{x \to +\infty} [e^{(x + 1)\ln{(1 + \frac{1}{x + 1})}} - e^{x\ln{(1 + \frac{1}{x})}}]
$$
$$
= \lim_{x \to \infty} {e^{(x + 1)[\frac{1}{x + 1} - \frac{1}{2(x + 1)^2} + \frac{1}{3(x + 1)^3}]} - e^{x[\frac{1}{x} - \frac{1}{2x^2} + \frac{1}{3x^3}]} }
$$
$$
= \lim_{x \to +\infty} {e^{[1 - \frac{1}{2(x + 1)} + \frac{1}{3(x + 1)^2}]} - e^{[1 - \frac{1}{2x} + \frac{1}{3x^2}]} }
$$
$$
无穷小量代换:e^{\alpha} - e^{\beta} = e^{\beta}(e^{\alpha - \beta} - 1) \sim e^{\beta}(\alpha - \beta) ,当 (\alpha - \beta) \to 0 时
$$
$$
=\lim_{x \to +\infty} e^{1 - \frac{1}{2x} + \frac{1}{3x^2}} [e^{\frac{1}{2x} - \frac{1}{2(x + 1)} - \frac{1}{3x^2} + \frac{1}{3(x + 1)^2}} - 1]
$$
$$
= \lim_{x \to +\infty} e [\frac{1}{2x(x + 1)} - \frac{2x + 1}{3x^2(x + 1)^2}]
$$
$$
原式 = \lim_{x \to +\infty}x^2 e [\frac{1}{2x(x + 1)} - \frac{2x + 1}{3x^2(x + 1)^2}]
$$
$$
= \lim_{x \to +\infty} e [\frac{x}{2(x + 1)} - \frac{2x + 1}{3(x + 1)^2}]
$$
$$
= \frac{e}{2}
$$
欧拉公式的证明
原文地址 zhuanlan.zhihu.com
由泰勒公式的麦克劳林公式展开可得:
$$
\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \cdots \
\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \cdots \
e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4} + \frac{x^5}{5!} + \cdots
$$
观察欧拉公式:
$$
e^{i \theta} = \cos \theta + i \sin \theta
$$
令 $x = i \theta$ 代入 $e^x$ 得:
$$
e^{i \theta} = 1 + i \theta - \frac{\theta^2}{2!} - \frac{i \theta^3}{3!} + \frac{\theta^4}{4!} + \frac{\theta^5}{5!} - \cdots ①
$$
令 $x = \theta$ 代入 $\cos x$ 得:
$$
\cos \theta = 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} - \cdots②
$$
令 $x = i \theta$ 代入 $\sin x$ 得:
$$ {③}
\sin \theta = \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} - \cdots ③
$$
即 ① = ② + ③ 可得:
$$
e^{i \theta} = \cos \theta + i \sin \theta
$$
巧记三角函数[和差化积]&[积化和差]
原文地址 zhuanlan.zhihu.com
和差化积公式
$$
\begin{align}
帅+帅=帅哥 \ \ \ \ \ & \sin \alpha + \sin \beta = 2\sin{\frac{\alpha+\beta}{2}}\cos{\frac{\alpha-\beta}{2}} \
帅-帅=哥帅 \ \ \ \ \ & \sin \alpha - \sin \beta = 2\cos{\frac{\alpha+\beta}{2}}\sin{\frac{\alpha-\beta}{2}} \
哥+哥=哥哥 \ \ \ \ \ & \cos \alpha + \cos \beta = 2\cos{\frac{\alpha+\beta}{2}}\cos{\frac{\alpha-\beta}{2}} \
哥-哥=负嫂嫂 \ \ & \cos \alpha - \cos \beta = -2\sin{\frac{\alpha+\beta}{2}}\sin{\frac{\alpha-\beta}{2}} \
\end{align}
$$
- 帅 + 帅 = 帅哥
- 帅 - 帅 = 哥帅
- 哥 + 哥 = 哥哥
- 哥 - 哥 = 负嫂嫂
积化和差公式
$$
\begin{align}
帅哥 = 帅 + 帅 \ \ \ \ \ &\sin \alpha \cos \beta = \frac{1}{2} [\sin{(\alpha+\beta)}+\sin{(\alpha-\beta)}] \
哥帅 = 帅 - 帅 \ \ \ \ \ &\cos \alpha \sin \beta = \frac{1}{2} [\sin{(\alpha+\beta)}-\sin{(\alpha-\beta)}] \
哥哥 = 哥 + 哥 \ \ \ \ \ &\cos \alpha \cos \beta = \frac{1}{2} [\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)}] \
负嫂嫂 = 哥 - 哥 \ \ &\sin \alpha \sin \beta = -\frac{1}{2} [\cos{(\alpha+\beta)}-\cos{(\alpha-\beta)}] \
\end{align}
$$
- 帅哥 = 帅 + 帅
- 哥帅 = 帅 - 帅
- 哥哥 = 哥 + 哥
- 负嫂嫂 = 哥 - 哥
前后相随,表里如一
前后相随(前后项数统一):
- 积是一项,化和差后要 $\div2$ ;
- 和差是两项,化积后要成 $\times 2$ 。
表里如一(内外项数统一):
- 括号内变量都是先 $\alpha + \beta$ ,再 $\alpha - \beta$ 。
- 化和差后是两项, $\alpha \pm \beta$ 两项不变;
- 化积后是一项, $\alpha \pm \beta$ 要 $\div2$ 变一项。
二维直角坐标旋转公式推导
原文地址 zhuanlan.zhihu.com
旋转公式
$$
\begin{cases}
x = x_0 \cos \theta - y_0 \sin \theta \
y = x_0 \sin \theta + y_0 \cos \theta
\end{cases}
$$
向量法基底法证明
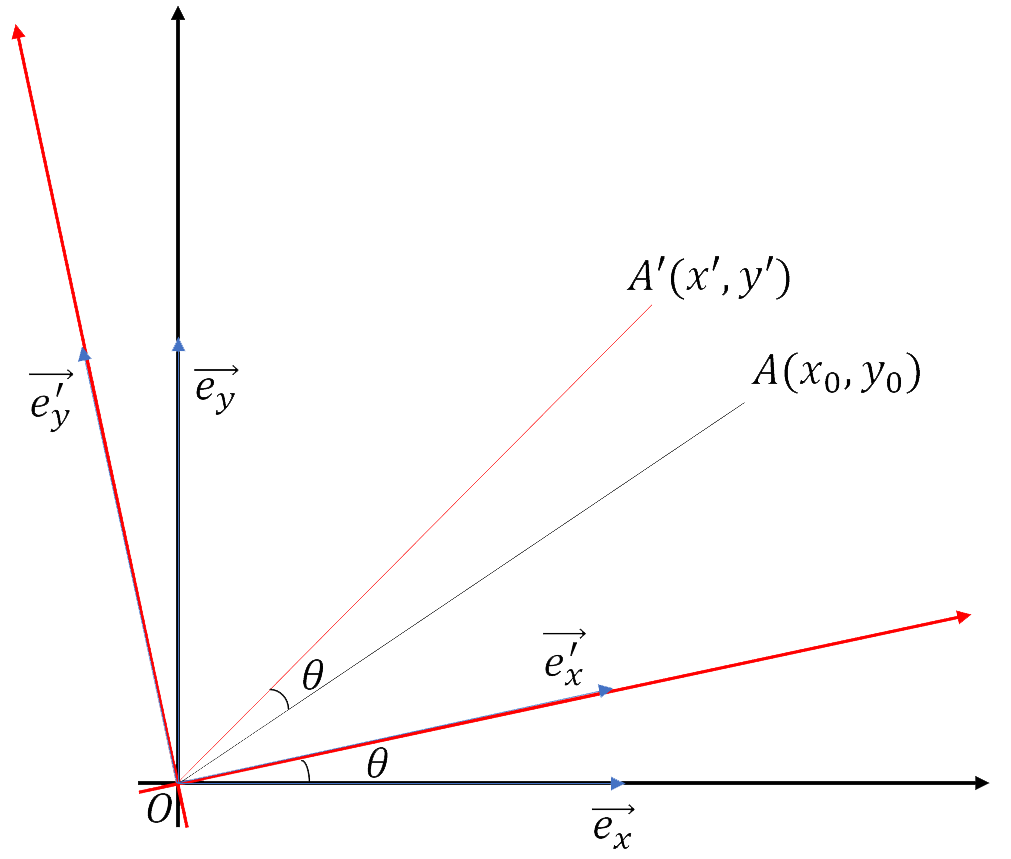
分别用基底向量表示:
$$
\begin{cases}
\vec{OA} = x \vec e_x + y \vec e_y \
\vec{OA’} = x \vec e’_x + y \vec e’_y
\end{cases}
$$
观察两对基底向量的几何关系可知:
$$
\begin{cases}
\vec e’_x = \vec e_x \cos \theta + \vec e_y \sin \theta \
\vec e’_y = -\vec e_x \sin \theta + \vec e_y \cos \theta
\end{cases}
$$
进一步推导可得:
$$
\begin{align}
\vec{OA’} &= x(\vec e_x \cos \theta + \vec e_y \sin \theta) + y(-\vec e_x \sin \theta + \vec e_y \cos \theta) \
&= (x \cos \theta - y \sin \theta) \vec e_x + (x \sin \theta + y \cos \theta) \vec e_y
\end{align}
$$
由此可得:
$$
\begin{cases}
x’ = x \cos \theta - y \sin \theta \
y’ = x \sin \theta + y \cos \theta
\end{cases}
$$
向量表示法证明
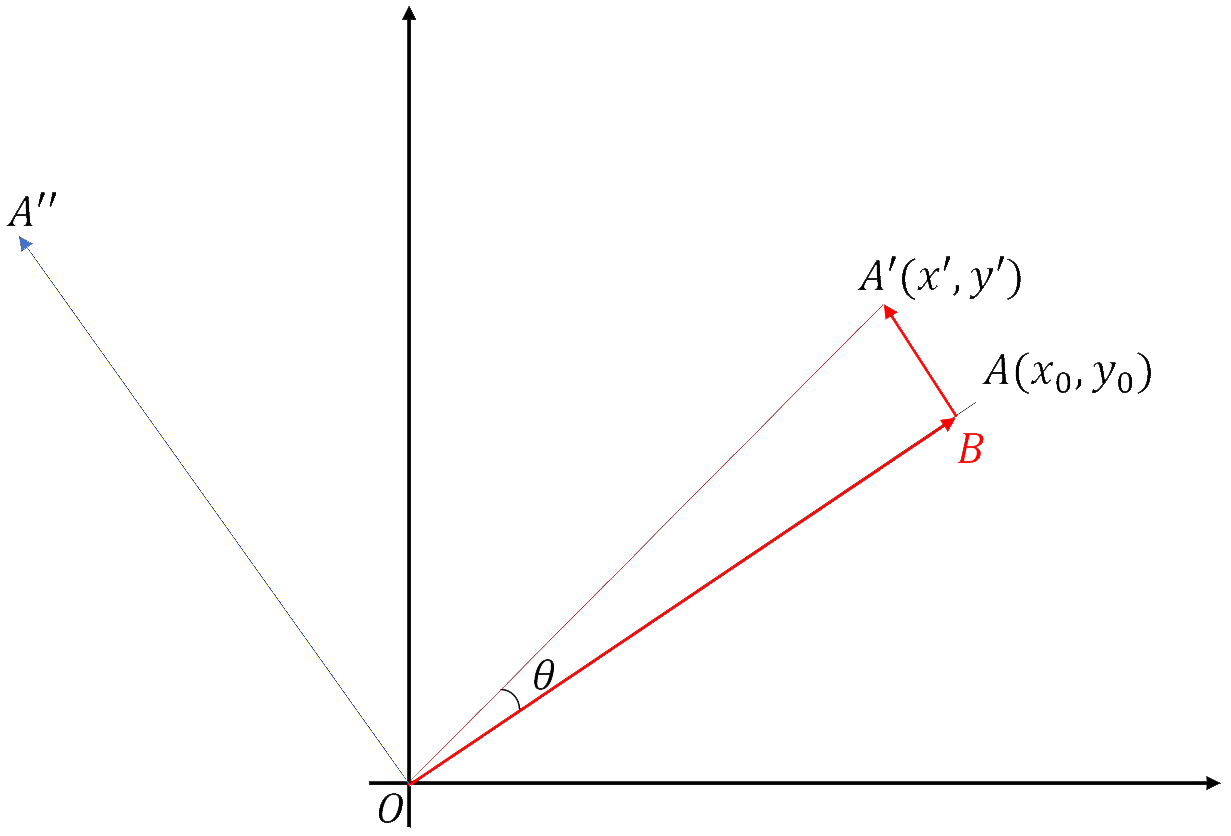
图中的$OA,OA’,OA’’$线段的长度均相等,其中$OA$与$OA’’$相垂直。
由几何关系可知:
$$
\vec{OA’} = \vec{OB} + \vec{BA’}
$$
进一步表示:
$$
\begin{align}
\vec{OA’} &= \vec{OB} + \vec{BA’} \
&= \frac{|\vec{OB}|}{|\vec{OA}|} \vec{OA} + \frac{|\vec{BA’}|}{|\vec{OA’’}|} \vec{OA’’} \
&= \frac{|\vec{OB}|}{\color{red}{|\vec{OA’}|}} \vec{OA} + \frac{|\vec{BA’}|}{\color{red}{|\vec{OA’}|}}\vec{OA’’} \
&= {\color{red}{\cos \theta}} \vec{OA} + {\color{red}{\sin \theta}} \vec{OA’’}
\end{align}
$$
由易知$\vec{OA},\vec{OA’},\vec{OA’’}$的向量坐标为:$(x,y),(x’,y’),(-y,x)$
$$
\begin{align}
(x’,y’) &= \cos \theta (x,y) + \sin \theta (-y,x) \
(x’,y’) &= (x \cos \theta -y \sin \theta,x \sin \theta + y \cos \theta)
\end{align}
$$
即可得:
$$
\begin{cases}
x’ = x \cos \theta - y \sin \theta \
y’ = x \sin \theta + y \cos \theta
\end{cases}
$$
复数表示法证明

一个复数乘$e^{i \theta}$相当于模不变逆时针方向旋转了$\theta$角。
欧拉公式:$e^{i \theta} = \cos \theta + i \sin \theta$
列出复数关系式并推导:
$$
\begin{align}
x’ + y’ i &= (x + y i) e^{i \theta} \
&= (x + y i)(\cos \theta + i \sin \theta) \
&= (x \cos \theta - y \sin \theta) + (x \sin \theta + y \cos \theta) i
\end{align}
$$
实部与实部相等,虚部与虚部相等:
$$
\begin{cases}
x’ = x \cos \theta - y \sin \theta \
y’ = x \sin \theta + y \cos \theta
\end{cases}
$$
Wallis公式推导与证明
原文地址 zhuanlan.zhihu.com
Wallis公式是通过一个无穷积表达式计算$\pi$的方法
$$
\begin{align}
\frac{\pi}{2} &= \prod_{n=1}^\infty \frac{4 n^2}{4n^2 - 1} = \prod_{n=1}^\infty (\frac{2n}{2n + 1} \cdot \frac{2n}{2n - 1}) \
&= (\frac{2}{1} \cdot \frac{2}{3})\cdot(\frac{4}{3} \cdot \frac{4}{5})\cdot(\frac{6}{5}\cdot\frac{6}{7})(\frac{8}{7}\cdot\frac{8}{9})\cdot \cdots
\end{align}
$$
或者
$$
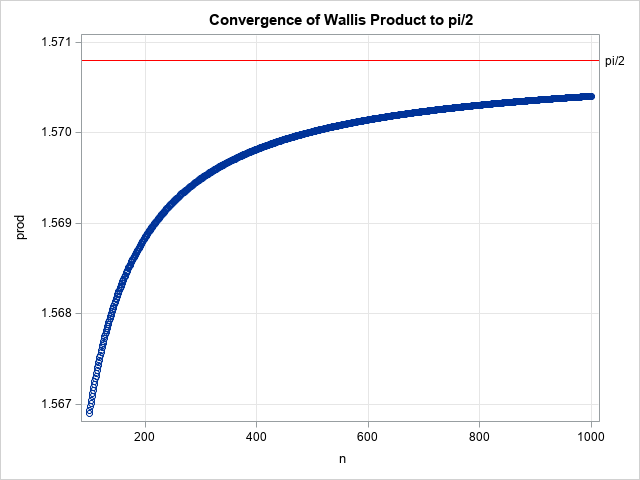
\lim_{n \to \infty} \frac{1}{2n + 1}[\frac{(2n)!!}{(2n - 1)!!}]^2 = \frac{\pi}{2}
$$
证明:
设 $I(n) = \int_0^{\frac{\pi}{2}} \sin^nx dx$
部分积分法拆分
$= \int_0^{\frac{\pi}{2}} \sin^{n - 1} x d (-\cos{x})$
$= \left.(-\cos x \sin^{n-1} x)\right|_0^{\frac{\pi}{2}} - \int_0^{\frac{\pi}{2}}(-\cos x)d \sin^{n-1} x$
$= \left.(-\cos x \sin^{n-1} x)\right|_0^{\frac{\pi}{2}} - \int_0^{\frac{\pi}{2}}(-\cos^2 x)(n - 1)\sin^{n-2} x dx$
$= (n - 1) \int_0^{\frac{\pi}{2}} \cos^2x \sin^{n-2}x dx$
$= (n - 1) \int_0^{\frac{\pi}{2}} (1 - \sin^2 x) \sin^{n-2}x dx$
$= (n - 1) \int_0^{\frac{\pi}{2}} (\sin^{n-2}x - \sin^n x) dx$
$= (n - 1) \int_0^{\frac{\pi}{2}} \sin^{n-2}x dx - (n - 1)\int_0^{\frac{\pi}{2}} \sin^n x dx$
$= (n - 1) I(n - 2) - (n - 1)I(n)$
$\Rightarrow I(n) = \frac{n - 1}{n} I (n - 2) \Rightarrow \begin{cases} \frac{I(2n + 1)} {I(2n - 1)} = \frac{2n}{2n + 1} \ \frac{I(2n)}{I(2n - 2)} = \frac{2n - 1}{2n} \end{cases}$
$\frac{I(3)}{I(1)} \cdot \frac{I(5)}{I(3)} \cdots \frac{I(2n + 1)}{I(2n - 1)} = \frac{2 \times 1}{2 \times 1 + 1} \times \frac{2 \times 2}{2 \times 2 + 1} \times \cdots \times \frac{2 n}{2n + 1} = \frac{(2n)!!}{(2n + 1)!!}$
$\frac{I(2)}{I(0)} \cdot \frac{I(4)}{I(2)} \cdots \frac{I(2n)}{I(2n - 2)} = \frac{2 \times 1 - 1}{2 \times 1} \times \frac{2 \times 2 - 1}{2 \times 2} \times \cdots \times \frac{2 n - 1}{2n} = \frac{(2n - 1)!!}{(2n)!!}$
左边的式子累称相消,最终得
$$
I(n) = \int_0^{\frac{\pi}{2}} \sin^n x dx = \begin{cases} \frac{\pi}{2} & n = 0 \ 1 & n =1 \ \frac{(2k)!!}{(2k + 1)!!} & n = 2k+1 \ \frac{(2k - 1)!!}{(2k)!!}\frac{\pi}{2} & n = 2k \end{cases}
$$
由 $\sin x$ 的单调性可知
$\sin^{2k + 1}x \leq \sin^{2k}x \leq \sin^{2k - 1}x,x\in [0,\frac{\pi}{2}]$
$\Downarrow$ 同时取定积分
$I(2k+1) < I(2k) < I(2k - 1)$
即得到
$\frac{(2k)!!}{(2k + 1)!!} < \frac{(2k - 1)!!}{(2k)!!} \frac{\pi}{2} < \frac{(2k - 2)!!}{(2k - 1)!!}$
$\frac{1}{2k+1} \cdot [\frac{(2k)!!}{(2k - 1)!!}]^2 < \frac{\pi}{2} < \frac{1}{2k} \cdot [\frac{(2k)!!}{(2k - 1)!!}]^2$
由夹逼定理可得
$\lim_{k \to \infty} \frac{1}{2k+1} \cdot [\frac{(2k)!!}{(2k - 1)!!}]^2 = \frac{\pi}{2}$
数据结构-二叉树入门Go语言实现
原文地址 zhuanlan.zhihu.com
之前我们一直在谈的是一对一的线性结构,可现实中,还有很多一对多的情况需要处理,所以我们需要研究这种一对多的数据结构——“树”,考虑它的各种特性,来解决我们在编程中碰到的相关问题。
树的定义
树(Tree)是 n(n≥0)个结点的有限集。n=0 时称为空树。在任意一棵非空树中:(1)有且仅有一个特定的称为_根(Root)_的结点;(2)当 n>1 时,其余结点可分为 m(m>0)个互不相交的有限集 T1 、T2 、……、Tm ,其中每一个集合本身又是一棵树,并且称为根的_子树(SubTree)_。
对于树的定义还需要强调两点:
- n>0 时根结点是唯一的,不可能存在多个根结点,别和现实中的大树混在一起,现实中的树有很多根须,那是真实的树,数据结构中的树是只能有一个根结点。
- m>0 时,子树的个数没有限制,但它们一定是互不相交的。像图 6-2-3 中的两个结构就不符合树的定义,因为它们都有相交的子树。
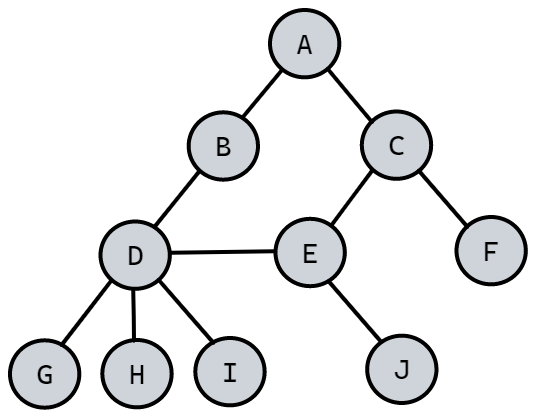

结点分类
树的结点包含一个数据元素及若干指向其子树的分支。结点拥有的子树数称为结点的_度(De-gree)_。度为 0 的结点称为_叶结点(Leaf)_或终端结点;度不为 0 的结点称为非终端结点或_分支结点_。除根结点之外,分支结点也称为内部结点。_树的度_是树内各结点的度的最大值。
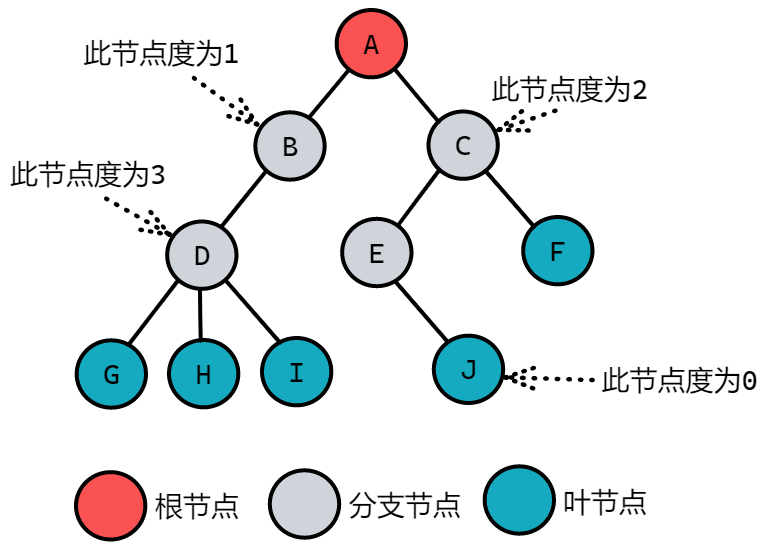
结点间关系
结点的子树的根称为该结点的_孩子(Child)_,相应地,该结点称为孩子的_双亲(Parent)_。嗯,为什么不是父或母,叫双亲呢?呵呵,对于结点来说其父母同体,唯一的一个,所以只能把它称为双亲了。同一个双亲的孩子之间互称_兄弟(Sibling)_。结点的_祖先_是从根到该结点所经分支上的所有结点。反之,以某结点为根的子树中的任一结点都称为该结点的_子孙_。
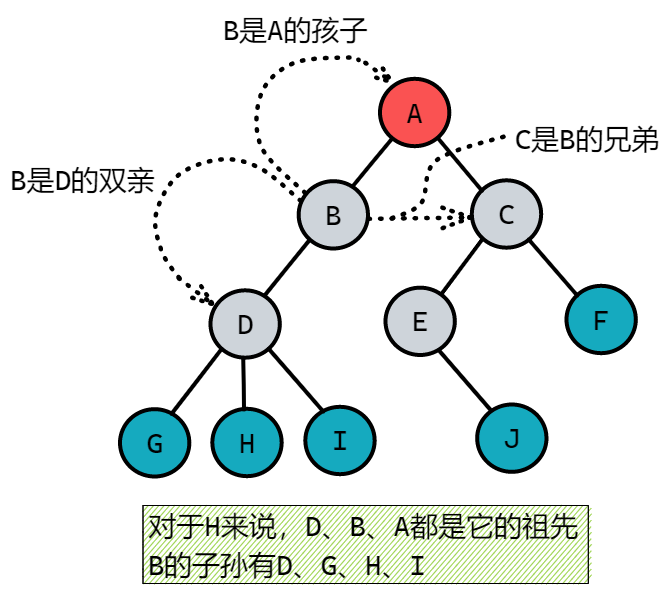
树的其他相关概念
结点的_层次(Level)_从根开始定义起,根为第一层,根的孩子为第二层。若某结点在第 l 层,则其子树就在第 l+1 层。其双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的_深度_(Depth)或高度。

如果将树中结点的各子树看成从左至右是有次序的,不能互换的,则称该树为_有序树_,否则称为_无序树_。
_森林_(Forest)是 m(m≥0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林。
树的抽象数据类型
相对于线性结构,树的操作就完全不同了,这里我们给出一些基本和常用操作。
1 | ADT // 树(tree) |
树的存储结构
说到存储结构,就会想到我们前面章节讲过的顺序存储和链式存储两种结构。
树中某个结点的孩子可以有多个,这就意味着,无论按何种顺序将树中所有结点存储到数组中,结点的存储位置都无法直接反映逻辑关系,简单的顺序存储结构是不能满足树的实现要求的。
不过充分利用顺序存储和链式存储结构的特点,完全可以实现对树的存储结构的表示。通常有三种不同的表示法:双亲表示法、孩子表示法、孩子兄弟表示法。需要高维顺序表,我们这里不展开讨论。
二叉树的定义
二叉树(Binary tree)是树形结构的一个重要类型。二叉树是 n 个有限元素的集合,该集合或者为空、或者由一个称为根(root)的元素及两个不相交的、被分别称为_左子树_和_右子树_的二叉树组成,是有序树。当集合为空时,称该二叉树为空二叉树。在二叉树中,一个元素也称作一个节点。
二叉树的五种基本形态

特殊二叉树
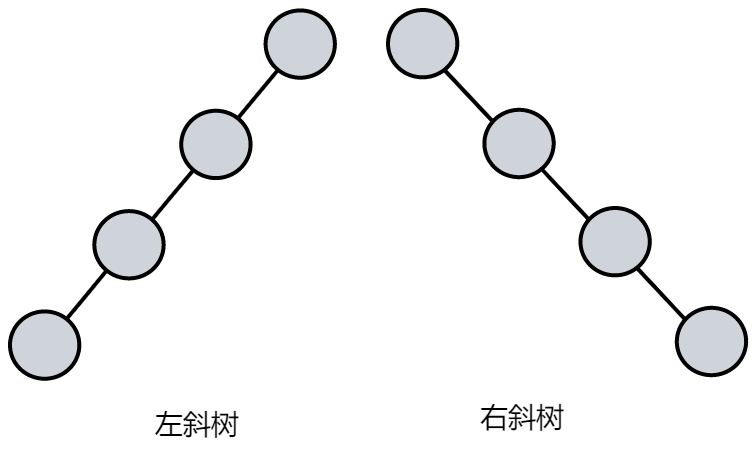
- 斜树
斜树一定要是斜的,所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。 - 满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。深度为 k 有 2k - 1 个结点的二叉树。 - 完全二叉树
对一棵具有 n 个结点的二叉树按层序编号,如果编号为 i(1≤i≤n)的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
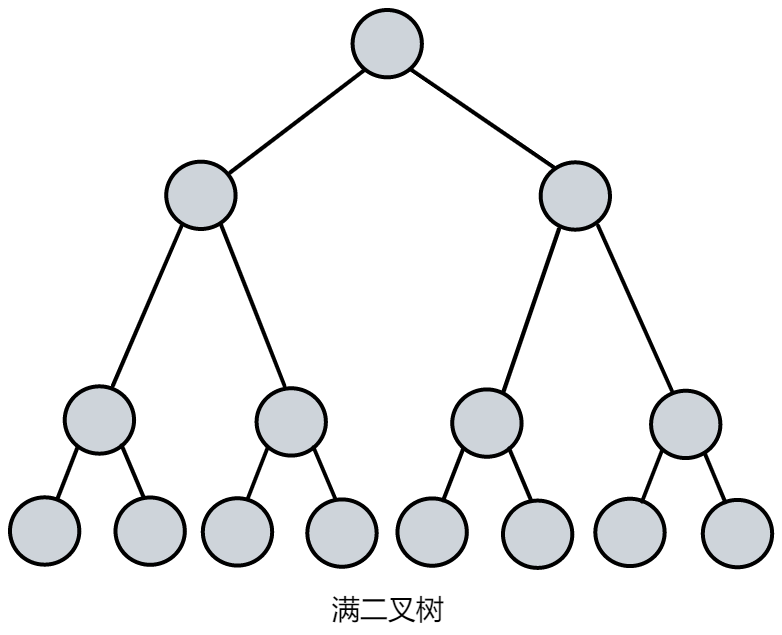
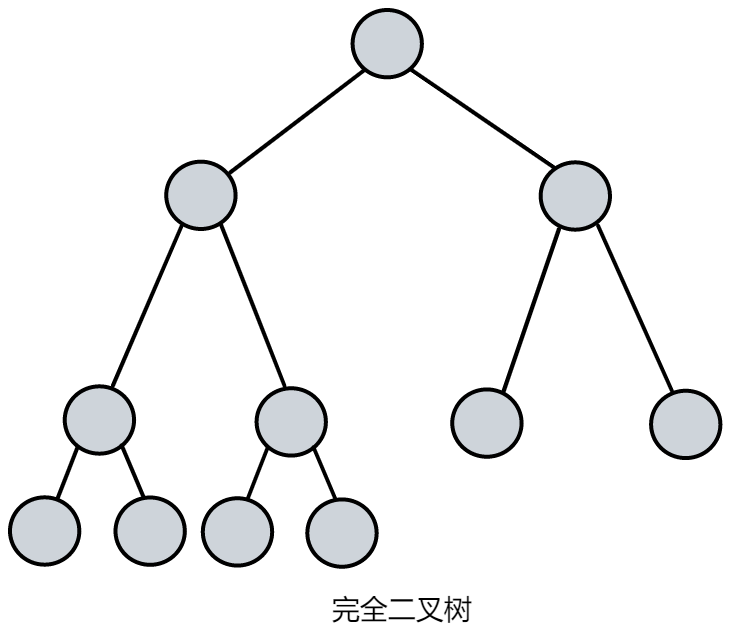
二叉树的性质
- 若二叉树结点的层次从 1 开始,则在二叉树第 i 层最多有 2i-1 (i> 0) 个节点。
- 深度为 k 的二叉树至少有 k 个结点,最多有 2i - 1 个结点。
- 对任何一个二叉树,如果其叶结点有 n0 个,度为 2 的非叶结点有 n2 个,则有 n0 = n2 + 1
- 具有 n 个结点的完全二叉树的深度为
- 如将一棵有 n 个结点的完全二叉树自顶向下,同一层自左向右连续给结点编号 1,2,…,n,则有以下关系:
- 若 i = 1,则 i 无双亲
- 若 i > 1,则双亲为
- 若 2i ≤ n,则 i 的左子女为 2i
- 若 2i+1 ≤ n,则 i 的右子女为 2i+1
- 若 i 为奇数,且 i≠1,其左兄弟为 i-1
- 若 1 为偶数,且 i≠n,其右兄弟为 i+1
二叉树的存储表示
顺序存储
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系等。

链式储存
二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。
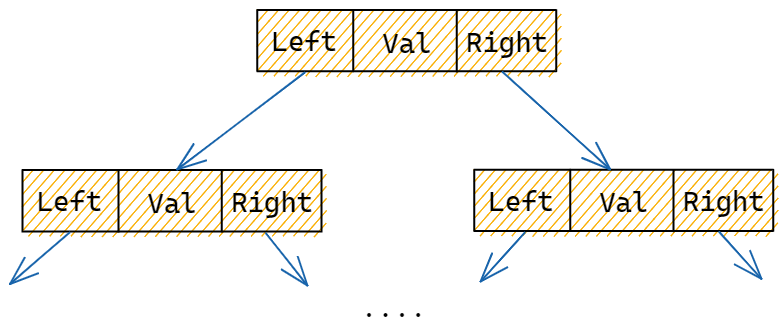
1 | type bt struct { |
二叉树的遍历
前序遍历
- V-L-R
1 | func preOrder(root *bt) { |
中序遍历
- L-V-R
1 | func inOrder(root *bt) { |
后序遍历
- L-R-V
1 | func posOrder(root *bt) { |
代码练习
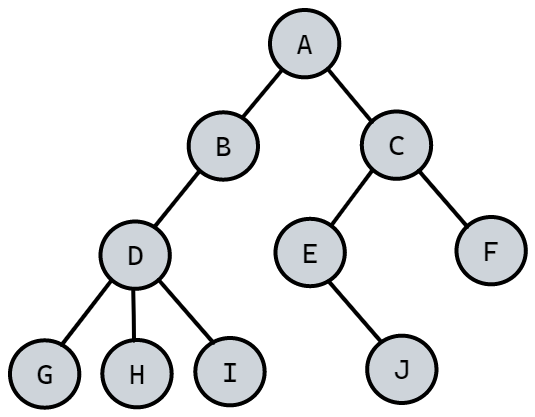
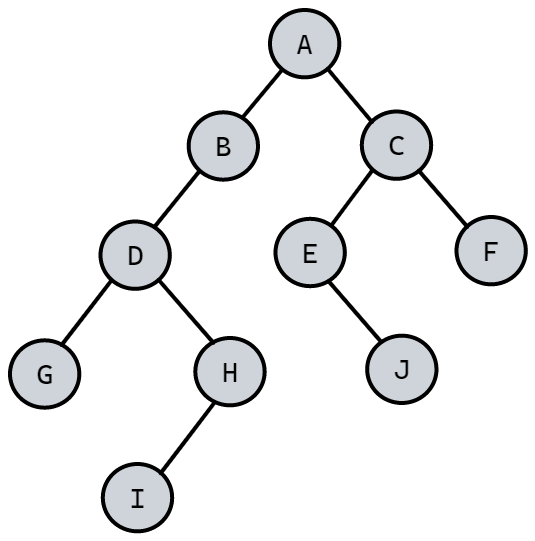
创建如下图所示的链式二叉树,并遍历。
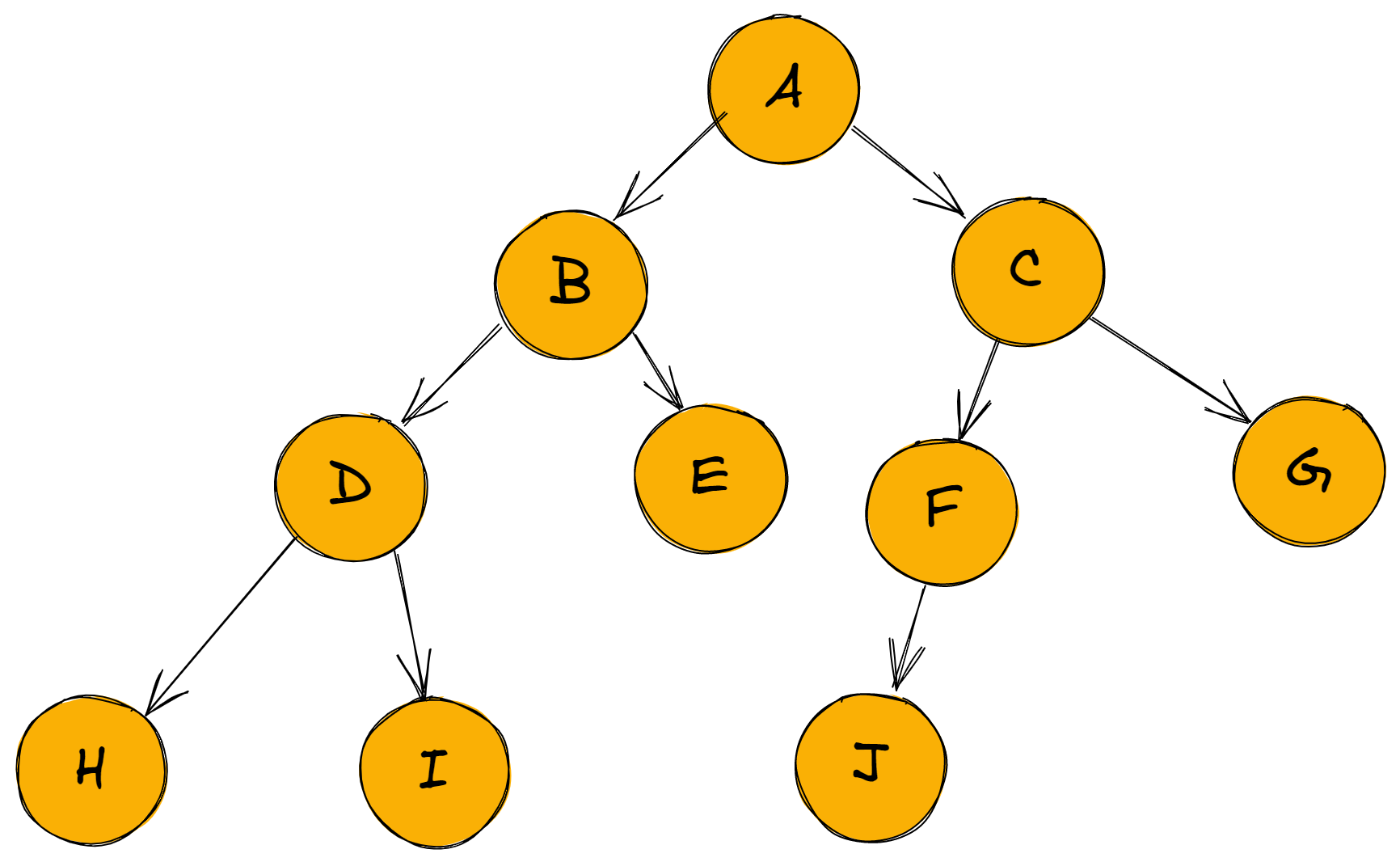
- 对于以上二叉树的创建可以直接通过节点之间的连接实现
- 此外我们还可以通过数组储存转为链式。
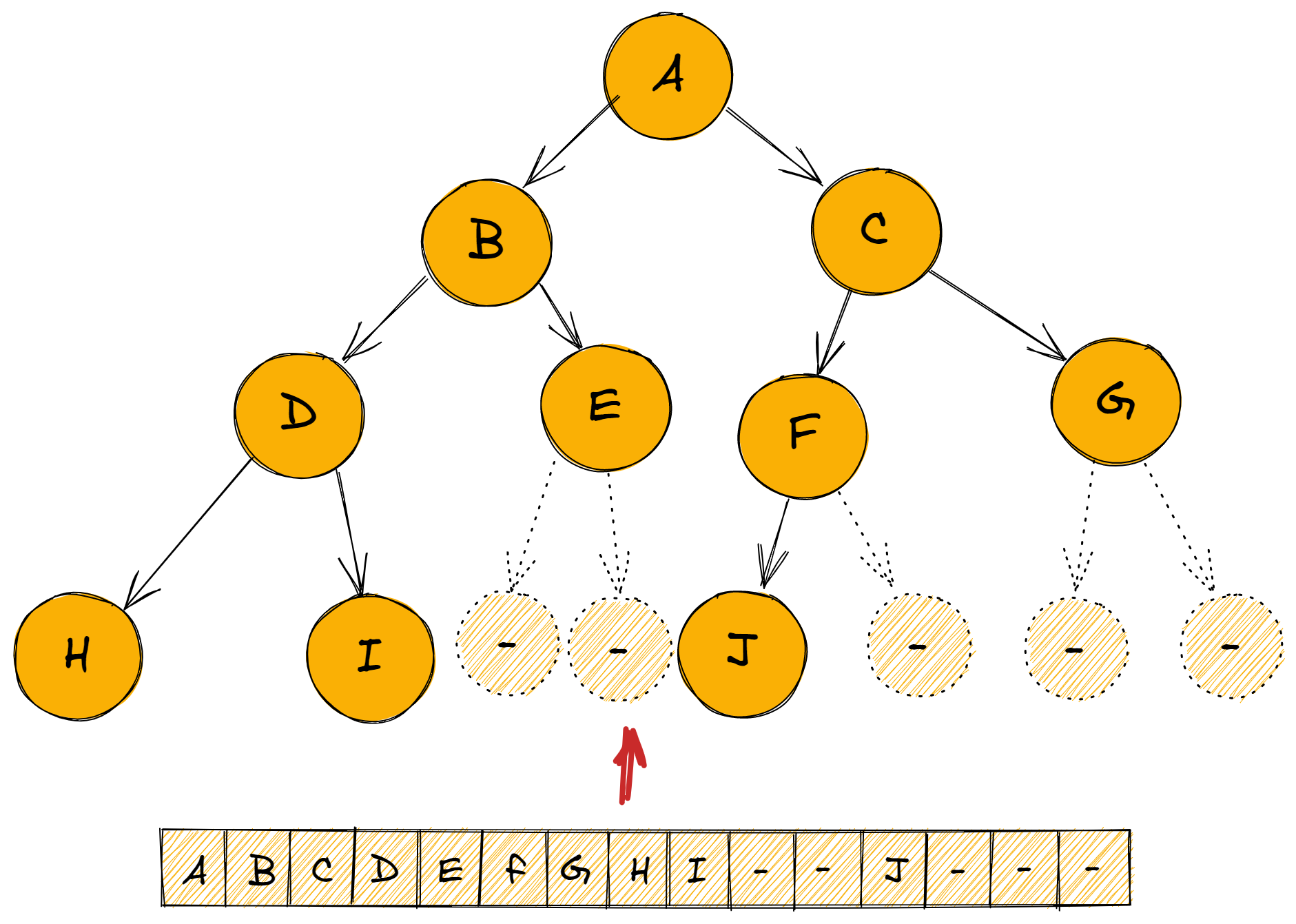
Go 语言代码参考
1 | package main |
二进制枚举简介 - Golang C++
原文地址 zhuanlan.zhihu.com
问题类型
有些问题的所有的可能状态数等于 $2^n$ (或者更多是 $2^n - 1$ ) 时,我们可以通过枚举遍历所有的可能状态,用二进制位运算来筛选符合我们条件的状态。
以下主要通过Go语言来演示,并附加参考的C++代码。这两种语言都很好的支持整数的二进制位运算与逻辑运算。
二进制:是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2,进位规则是“逢二进一”,借位规则是“借一当二”。
子集:是一个数学概念:如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集。
- 含有0个元素的子集有 $C_n^0$ 个,
- 含有1个元素的子集有 $C_n^1$ 个,
- 含有2个元素的子集有 $C_n^2$ 个,
- ………
- 含有N个元素的子集有 $C_n^n$ 个
由二项式系数的性质可得:$C_n^0 + c_n^1 + C_n^2 + \dots + C_n^n = 2^n$
二进制左移位运算: $1<<n = 2^n$
1<<0=1(0);
1<<1=2(10);
1<<2=4(100);
1<<3=8(1000);
1<<4=16(10000);
…
1<<7=128(10000000);
…
整体框架
Golang
1 | for i := 0; i < 1<<n; i++ { // 遍历枚举每一种可能的状态 |
C++
1 | for(int i = 0; i < (1<<n); i++) // 从0~2^n-1个状态 |
具体含义 (Go)
第一层循环:如果该问题的通过排列组合分析所有枚举情况有 $2^n$ 种(如果不存在全0的情况,即 $2^n - 1$ 种时,i 初始化为 1),则是这样的最外层循环枚举:
i 不仅实现了所有可能的循环次数,它的二进制表示还枚举了所有可能的状态。
1 | for i := 0; i < 1<<n; i++ { |
第二层循环:当进入某个具体的状态时 (进入第一层循环后),我们需要通过遍历每一位整数的二进制做逻辑与运算来搞清楚此状态具体情况。
假设有 5 个字母:A,B,C,D,E. 要从中至少选出一个,请问有哪些种选法?
举出其中一个可能状态,并用二进制表示:
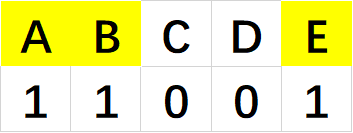
此时的外循环变量 $i = 1\times 2^4 + 1\times 2^3 + 1\times 2^0 = 25$ 此时列举 j = 0 的情况,1<<j 是在第 j 位为 1 其他均为 0 的二进制
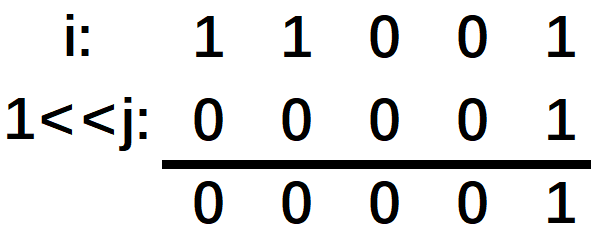
如果 i & (1<<j) >0 就说明循环变量 i 的二进制第 j 位数为 1,其含义是这个选择状态下字母 E 被选中。 同样道理遍历整个循环变量 i 的二进制每一位,来搞清楚它具体指什么情况。即 i & (1<j) 表达式的值仅由我们想要知道的 i 二进制下的第 j 位决定。 要注意 Go 语言整数型 int 不可直接转为布尔值,所以 i & (1<<j) >0 来表达。
1 | for j := 0; j < n; j++ { |
具体案例分析
和为 T(二进制枚举模板)
问题描述
从一个大小为 nums 的数组中选取一些元素,使得它们的和等于给定的值 target。每个元素限选一次,不能一个都不选。
样例输出
1 | nums = [-7, -3, -2, 5, 9] |
样例输出
1 | 打印输出: |
思路
这个问题很明显所有可能为 $2^n - 1$ 个,因为不能一个都不拿。所以就直接用 i 的二进制还模拟所有可能的选择情况。 当选项中有满足合为 target 的情况时输出并计数。
Golang
1 | package main |
C++ 仅供参考解决思路
1 | #include <bits/stdc++.h> |