原文地址 zhuanlan.zhihu.com
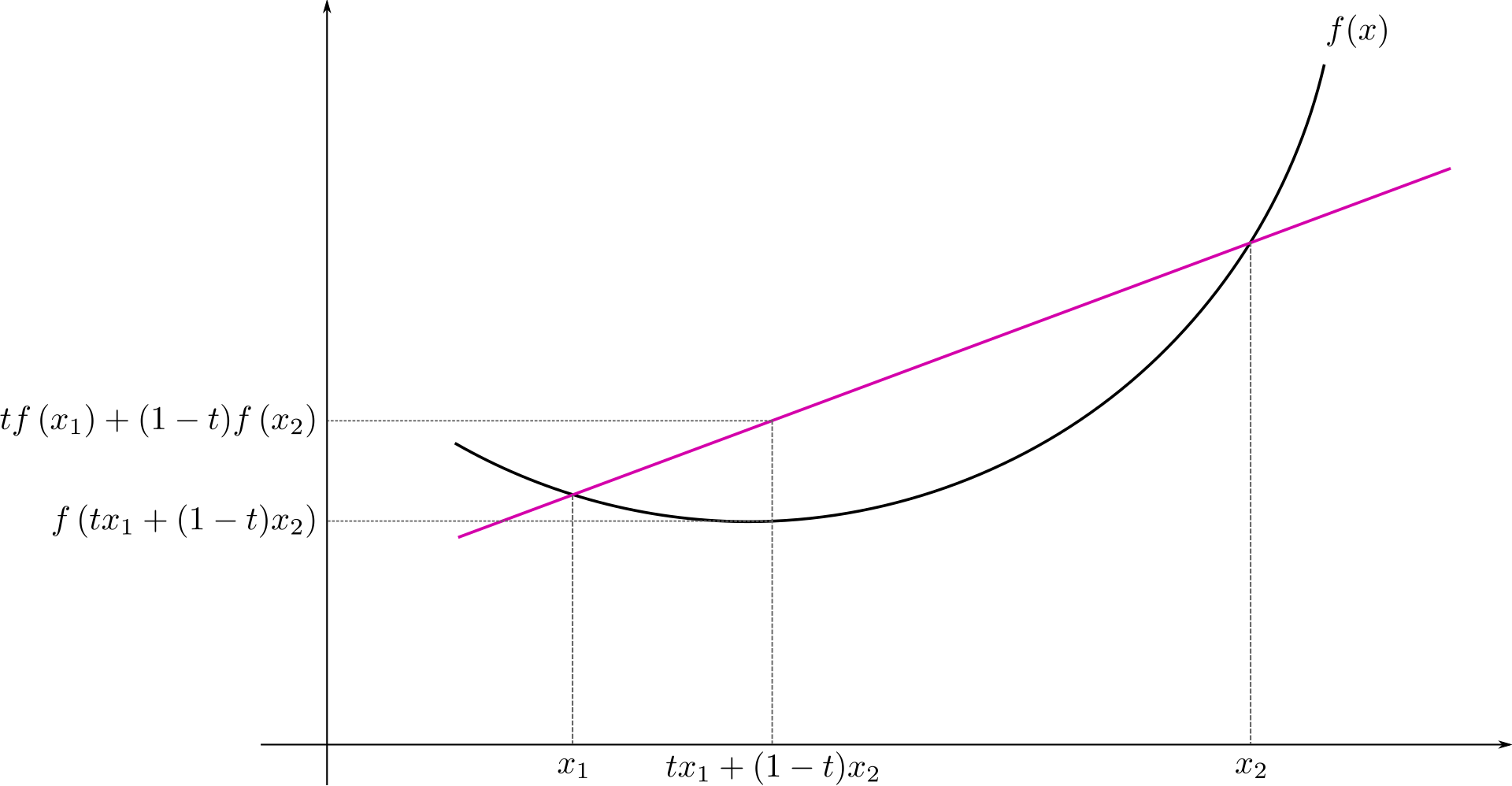
琴生不等式
若 $f(x)$ 是区间 $[a,b]$ 上的下凸函数,则对任意的 $x_1,x_2,\dots,x_n \in [a,b]$,则有不等式:
$$
\frac{\sum_{i = 1}^n f(x_i)}{n} \geq f(\frac{\sum_{i = 1}^n x_i}{n})
$$
当且仅当 $x_1 = x_2 = x_3 = \dots = x_n$ 时等号成立
均值不等式
对于若干个非负数 $x_1,x_2,\dots,x_n$ 有不等式:
$$
\frac{\sum_{i = 1}^n x_i}{n} \geq \sqrt[n]{\prod_{i=1}^n x_i}
$$
当且仅当 $x_1 = x_2 = x_3 = \dots = x_n$ 时等号成立
证明:
设 $f(x) = -\ln x , x > 0$
$f’(x) = -\frac{1}{x} , f’’(x) = \frac{1}{x^2} > 0$
即 $f(x)$ 为下凸函数,应用琴生不等式可得
$\frac{f(x_1) + f(x_2) + \dots + f(x_n)}{n} \geq f(\frac{x_1 + x_2 + \dots + x_n}{n})$
$- \frac{\ln x_1 + \ln x_2 + \dots + \ln x_n}{n} \geq - \ln(\frac{x_1 + x_2 + \dots + x_n}{n})$
$\frac{\ln{(x_1 x_2 \dots x_n)}}{n} \leq \ln{(\frac{x_1 + x_2 + \dots + x_n}{n})}$
$\ln{(x_1 x_2 \dots x_n)^{\frac{1}{n}}} \leq \ln{(\frac{x_1 + x_2 + \dots + x_n}{n})}$
$(x_1 x_2 \dots x_n)^{\frac{1}{n}} \leq \frac{x_1 + x_2 + \dots + x_n}{n}$
则 $\frac{\sum_{i = 1}^n x_i}{n} \geq \sqrt[n]{\prod_{i=1}^n x_i}$
证毕