二进制枚举简介 - Golang C++

Posted on | In , ,

原文地址 zhuanlan.zhihu.com

问题类型

有些问题的所有的可能状态数等于 $2^n$ (或者更多是 $2^n - 1$ ) 时，我们可以通过枚举遍历所有的可能状态，用二进制位运算来筛选符合我们条件的状态。

以下主要通过Go语言来演示，并附加参考的C++代码。这两种语言都很好的支持整数的二进制位运算与逻辑运算。

二进制：是计算技术中广泛采用的一种数制。二进制数据是用0和1两个数码来表示的数。它的基数为2，进位规则是“逢二进一”，借位规则是“借一当二”。

子集：是一个数学概念：如果集合A的任意一个元素都是集合B的元素，那么集合A称为集合B的子集。

  • 含有0个元素的子集有 $C_n^0$ 个，
  • 含有1个元素的子集有 $C_n^1$ 个，
  • 含有2个元素的子集有 $C_n^2$ 个，
  • ………
  • 含有N个元素的子集有 $C_n^n$ 个

由二项式系数的性质可得：$C_n^0 + c_n^1 + C_n^2 + \dots + C_n^n = 2^n$

二进制左移位运算： $1<<n = 2^n$

1<<0=1(0);
1<<1=2(10);
1<<2=4(100);
1<<3=8(1000);
1<<4=16(10000);
…
1<<7=128(10000000);
…

整体框架

Golang

1
2
3
4
5
6
7
8
9
10
11
for i := 0; i < 1<<n; i++ {  // 遍历枚举每一种可能的状态
    for j := 0; j < n; j++ { // 检查当前状态情况
        if i & (1<<j) > 0 {  // 做二进制逻辑运算
            记录该状态
        }
    }
    if 状态i满足我们的要求 {
        保存该状态
    }
}
return 满足要求足的状态集或状态数目

C++

1
2
3
4
5
6
7
8
9
10
11
12
for(int i = 0; i < (1<<n); i++) // 从0～2^n-1个状态
{
    for(int j = 0; j < n; j++) // 遍历二进制的每一位
    {
        if(i & (1 << j))// 判断二进制第j位是否存在
        {
            printf("%d ",j);// 如果存在输出第j个元素
        }
    }
    // 后续处理
}
return 满足要求足的状态集或状态数目;

具体含义 (Go)

第一层循环：如果该问题的通过排列组合分析所有枚举情况有 $2^n$ 种（如果不存在全0的情况，即 $2^n - 1$ 种时，i 初始化为 1），则是这样的最外层循环枚举：

i 不仅实现了所有可能的循环次数，它的二进制表示还枚举了所有可能的状态。

1
2
3
for i := 0; i < 1<<n; i++ {
    ...
}

第二层循环：当进入某个具体的状态时 (进入第一层循环后)，我们需要通过遍历每一位整数的二进制做逻辑与运算来搞清楚此状态具体情况。

假设有 5 个字母：A,B,C,D,E. 要从中至少选出一个，请问有哪些种选法？

举出其中一个可能状态，并用二进制表示：

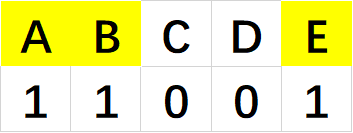
此时的外循环变量 $i = 1\times 2^4 + 1\times 2^3 + 1\times 2^0 = 25$ 此时列举 j = 0 的情况，1<<j 是在第 j 位为 1 其他均为 0 的二进制

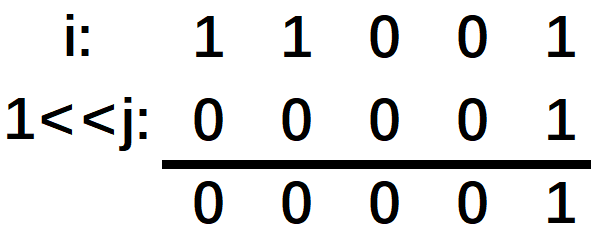
如果 i & (1<<j) >0 就说明循环变量 i 的二进制第 j 位数为 1，其含义是这个选择状态下字母 E 被选中。 同样道理遍历整个循环变量 i 的二进制每一位，来搞清楚它具体指什么情况。即 i & (1<j) 表达式的值仅由我们想要知道的 i 二进制下的第 j 位决定。 要注意 Go 语言整数型 int 不可直接转为布尔值，所以 i & (1<<j) >0 来表达。

1
2
3
4
5
for j := 0; j < n; j++ {
    if i & (1<<j) > 0 {
        ...
    }
}

具体案例分析

和为 T（二进制枚举模板）

问题描述

从一个大小为 nums 的数组中选取一些元素，使得它们的和等于给定的值 target。每个元素限选一次，不能一个都不选。

样例输出

1
2
nums = [-7, -3, -2, 5, 9]
target = 0

样例输出

1
2
3
4
打印输出：
-3      -2      5
-7      -2      9
返回值：2

思路

这个问题很明显所有可能为 $2^n - 1$ 个，因为不能一个都不拿。所以就直接用 i 的二进制还模拟所有可能的选择情况。 当选项中有满足合为 target 的情况时输出并计数。

Golang

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
package main
​
import "fmt"
​
func sumTarget(nums []int, target int) int {
    var sum int
    n := len(nums)
    res := 0
    for i := 1; i < 1<<n; i++ {
        sum = 0
        for j := 0; j < n; j++ {
            if i&(1<<j) > 0 {
                sum += nums[j]
            }
        }
        if sum == target {
            res++
            for j := 0; j < n; j++ {
                if i&(1<<j) > 0 {
                    fmt.Printf("%d\t", nums[j])
                }
            }
            fmt.Println()
        }
    }
    return res
}
​
func main() {
    nums := []int{-7, -3, -2, 5, 9}
    target := 0
    fmt.Println(sumTarget(nums, target))
}
/*
-3      -2      5
-7      -2      9
2
*/

C++ 仅供参考解决思路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <bits/stdc++.h>
using namespace std;
int main()
{
    int n,target;
    int sum = 0;
    int count = 0;
    cin >> n;
    int nums[n];
    for(int i = 0; i < n; i++)cin >> nums[i];
    cin >> target;
    for(int i = 1; i < (1<<n); i++) //从0～2^n-1个状态
    {
        sum = 0;
        for(int j = 0; j < n; j++) //遍历二进制的每一位
        {
            if(i & (1 << j))//判断二进制第j位是否存在
            {
                sum += nums[j];//如果存在输出第j个元素
            }
        }
        if(sum == target)
        {
            count++; //计数
            for(int j = 0; j < n; j++)
            {
                if(i & (1 << j))//判断二进制第j位是否存在
                {
                    cout << nums[j] << "\t";
                }
            }
            cout << endl;
        }
    }
    cout << count;
    return 0;
}
/*
5
-1 3 2 -5 1
0
3       2       -5
-1      1
-1      3       2       -5      1
3
*/