数据结构-二叉树入门Go语言实现

原文地址 zhuanlan.zhihu.com

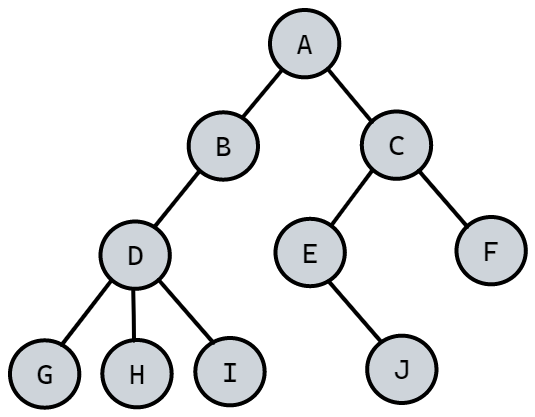
之前我们一直在谈的是一对一的线性结构，可现实中，还有很多一对多的情况需要处理，所以我们需要研究这种一对多的数据结构——“树”，考虑它的各种特性，来解决我们在编程中碰到的相关问题。

树的定义

树（Tree）是 n（n≥0）个结点的有限集。n=0 时称为空树。在任意一棵非空树中：（1）有且仅有一个特定的称为_根（Root）_的结点；（2）当 n＞1 时，其余结点可分为 m（m＞0）个互不相交的有限集 T1 、T2 、……、Tm ，其中每一个集合本身又是一棵树，并且称为根的_子树（SubTree）_。

对于树的定义还需要强调两点：

1. n>0 时根结点是唯一的，不可能存在多个根结点，别和现实中的大树混在一起，现实中的树有很多根须，那是真实的树，数据结构中的树是只能有一个根结点。
2. m>0 时，子树的个数没有限制，但它们一定是互不相交的。像图 6-2-3 中的两个结构就不符合树的定义，因为它们都有相交的子树。

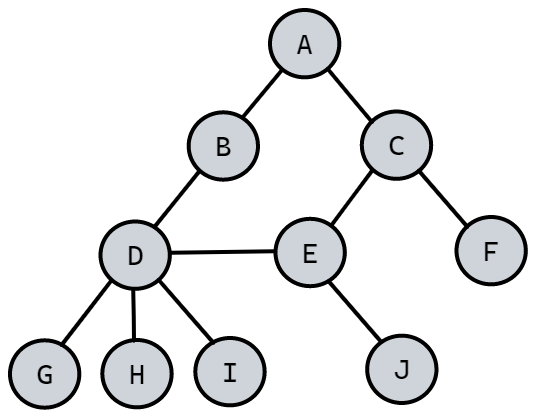
结点分类

树的结点包含一个数据元素及若干指向其子树的分支。结点拥有的子树数称为结点的_度（De-gree）_。度为 0 的结点称为_叶结点（Leaf）_或终端结点；度不为 0 的结点称为非终端结点或_分支结点_。除根结点之外，分支结点也称为内部结点。_树的度_是树内各结点的度的最大值。

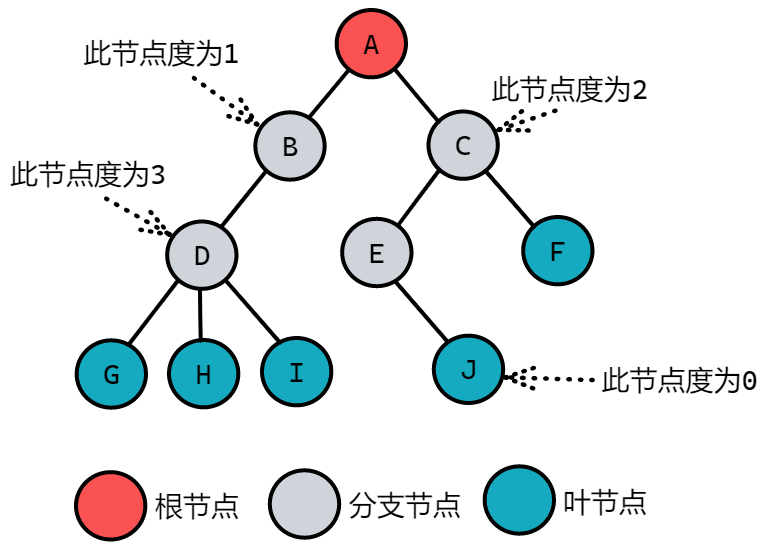
结点间关系

结点的子树的根称为该结点的_孩子（Child）_，相应地，该结点称为孩子的_双亲（Parent）_。嗯，为什么不是父或母，叫双亲呢？呵呵，对于结点来说其父母同体，唯一的一个，所以只能把它称为双亲了。同一个双亲的孩子之间互称_兄弟（Sibling）_。结点的_祖先_是从根到该结点所经分支上的所有结点。反之，以某结点为根的子树中的任一结点都称为该结点的_子孙_。

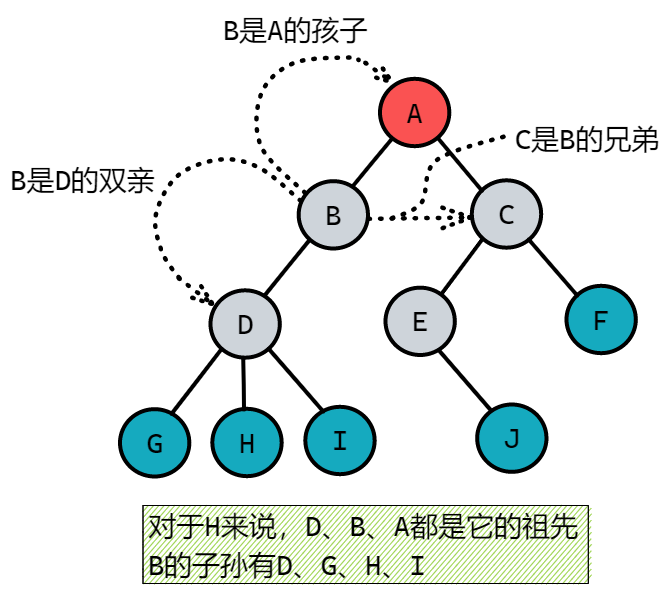
树的其他相关概念

结点的_层次（Level）_从根开始定义起，根为第一层，根的孩子为第二层。若某结点在第 l 层，则其子树就在第 l+1 层。其双亲在同一层的结点互为堂兄弟。树中结点的最大层次称为树的_深度_（Depth）或高度。

如果将树中结点的各子树看成从左至右是有次序的，不能互换的，则称该树为_有序树_，否则称为_无序树_。

_森林_（Forest）是 m（m≥0）棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。

树的抽象数据类型

相对于线性结构，树的操作就完全不同了，这里我们给出一些基本和常用操作。

ADT // 树(tree)
Data    // 树是由一个根结点和若干棵子树构成。树中结点具有相同数据类型及层次关系。
Operation
    // 构造空树T。
    InitTree(*T):
    // 销毁树T。
    DestroyTree(*T):
    // 按definition中给出树的定义来构造树。
    CreateTree(*T, definition):
    // 若树T存在，则将树T清为空树。
    ClearTree(*T):
    // 若T为空树，返回true，否则返回false。
    TreeEmpty(T):
    // 返回T的深度。
    TreeDepth(T):
    // 返回T的根结点。
    Root(T):
    // cur_e是树T中一个结点，返回此结点的值。
    Value(T, cur_e):
    // 给树T的结点cur_e赋值为value。
    Assign(T, cur_e, value):
    // 若cur_e是树T的非根结点，则返回它的双亲，否则返回空。
    Parent(T, cur_e):
    // 若cur_e是树T的非叶结点，则返回它的最左孩子，否则返回空。
    LeftChild(T, cur_e):
    // 若cur_e有右兄弟，则返回它的右兄弟，否则返回空。
    RightSibling(T, cur_e):
    // 其中p指向树T的某个结点，i为所指结点p的度加上1，非空树c与T不相交，操作结果为插入c为树T中p指结点的第i棵子树。
    InsertChild(*T, *p, i, c):
    // 其中p指向树T的某个结点，i为所指结点p的度，操作结果为删除T中p所指结点的第i棵子树。
    DeleteChild(*T, *p, i):
endADT

树的存储结构

说到存储结构，就会想到我们前面章节讲过的顺序存储和链式存储两种结构。

树中某个结点的孩子可以有多个，这就意味着，无论按何种顺序将树中所有结点存储到数组中，结点的存储位置都无法直接反映逻辑关系，简单的顺序存储结构是不能满足树的实现要求的。

不过充分利用顺序存储和链式存储结构的特点，完全可以实现对树的存储结构的表示。通常有三种不同的表示法：双亲表示法、孩子表示法、孩子兄弟表示法。需要高维顺序表，我们这里不展开讨论。

二叉树的定义

二叉树（Binary tree）是树形结构的一个重要类型。二叉树是 n 个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为_左子树_和_右子树_的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点。

二叉树的五种基本形态

特殊二叉树

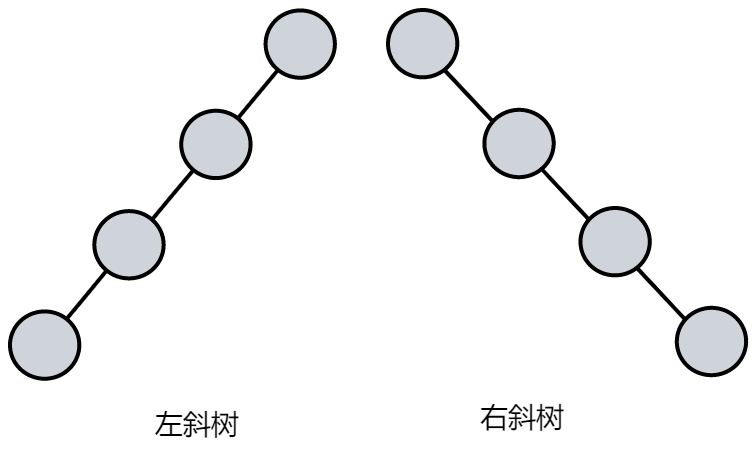
1. 斜树
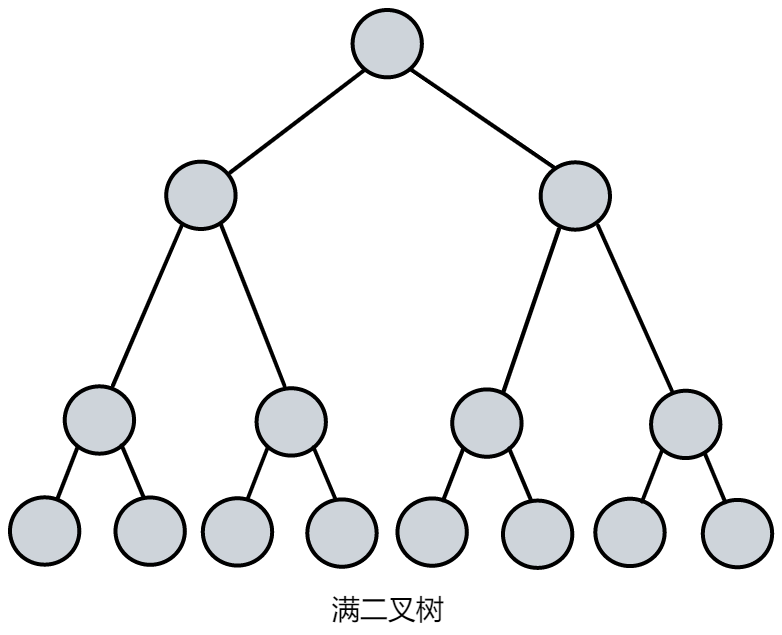
   斜树一定要是斜的，所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。
2. 满二叉树
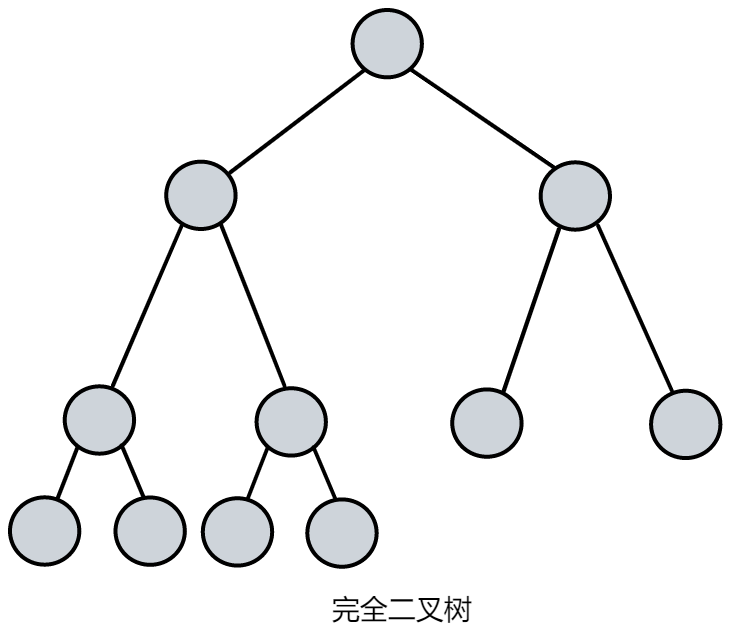
   在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。深度为 k 有 2k - 1 个结点的二叉树。
3. 完全二叉树
   对一棵具有 n 个结点的二叉树按层序编号，如果编号为 i（1≤i≤n）的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

二叉树的性质

1. 若二叉树结点的层次从 1 开始，则在二叉树第 i 层最多有 2i-1 (i> 0) 个节点。
2. 深度为 k 的二叉树至少有 k 个结点，最多有 2i - 1 个结点。
3. 对任何一个二叉树，如果其叶结点有 n0 个，度为 2 的非叶结点有 n2 个，则有 n0 = n2 + 1
4. 具有 n 个结点的完全二叉树的深度为
5. 如将一棵有 n 个结点的完全二叉树自顶向下，同一层自左向右连续给结点编号 1,2,…，n，则有以下关系:

• 若 i = 1，则 i 无双亲
• 若 i > 1，则双亲为
• 若 2i ≤ n，则 i 的左子女为 2i
• 若 2i+1 ≤ n，则 i 的右子女为 2i+1
• 若 i 为奇数，且 i≠1，其左兄弟为 i-1
• 若 1 为偶数，且 i≠n，其右兄弟为 i+1

二叉树的存储表示

顺序存储

二叉树的顺序存储结构就是用一维数组存储二叉树中的结点，并且结点的存储位置，也就是数组的下标要能体现结点之间的逻辑关系，比如双亲与孩子的关系，左右兄弟的关系等。

链式储存

二叉树每个结点最多有两个孩子，所以为它设计一个数据域和两个指针域是比较自然的想法，我们称这样的链表叫做二叉链表。

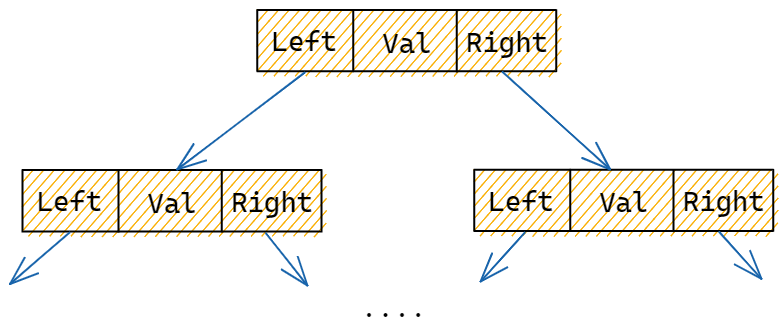
type bt struct {
    Val   string
    Left  *bt
    Right *bt
}

二叉树的遍历

前序遍历

• V-L-R

func preOrder(root *bt) {
    if root != nil {
        fmt.Print(root.Val, " ")
        preOrder(root.Left)
        preOrder(root.Right)
    }
}

中序遍历

• L-V-R

func inOrder(root *bt) {
    if root != nil {
        inOrder(root.Left)
        fmt.Print(root.Val, " ")
        inOrder(root.Right)
    }
}

后序遍历

• L-R-V

func posOrder(root *bt) {
    if root != nil {
        posOrder(root.Left)
        posOrder(root.Right)
        fmt.Print(root.Val, " ")
    }
}

代码练习

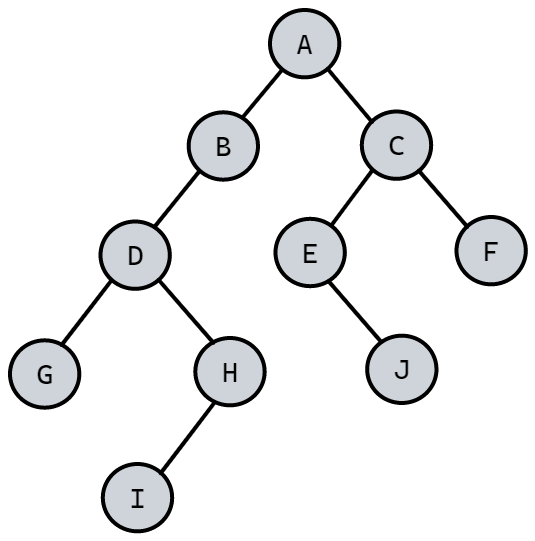
创建如下图所示的链式二叉树，并遍历。

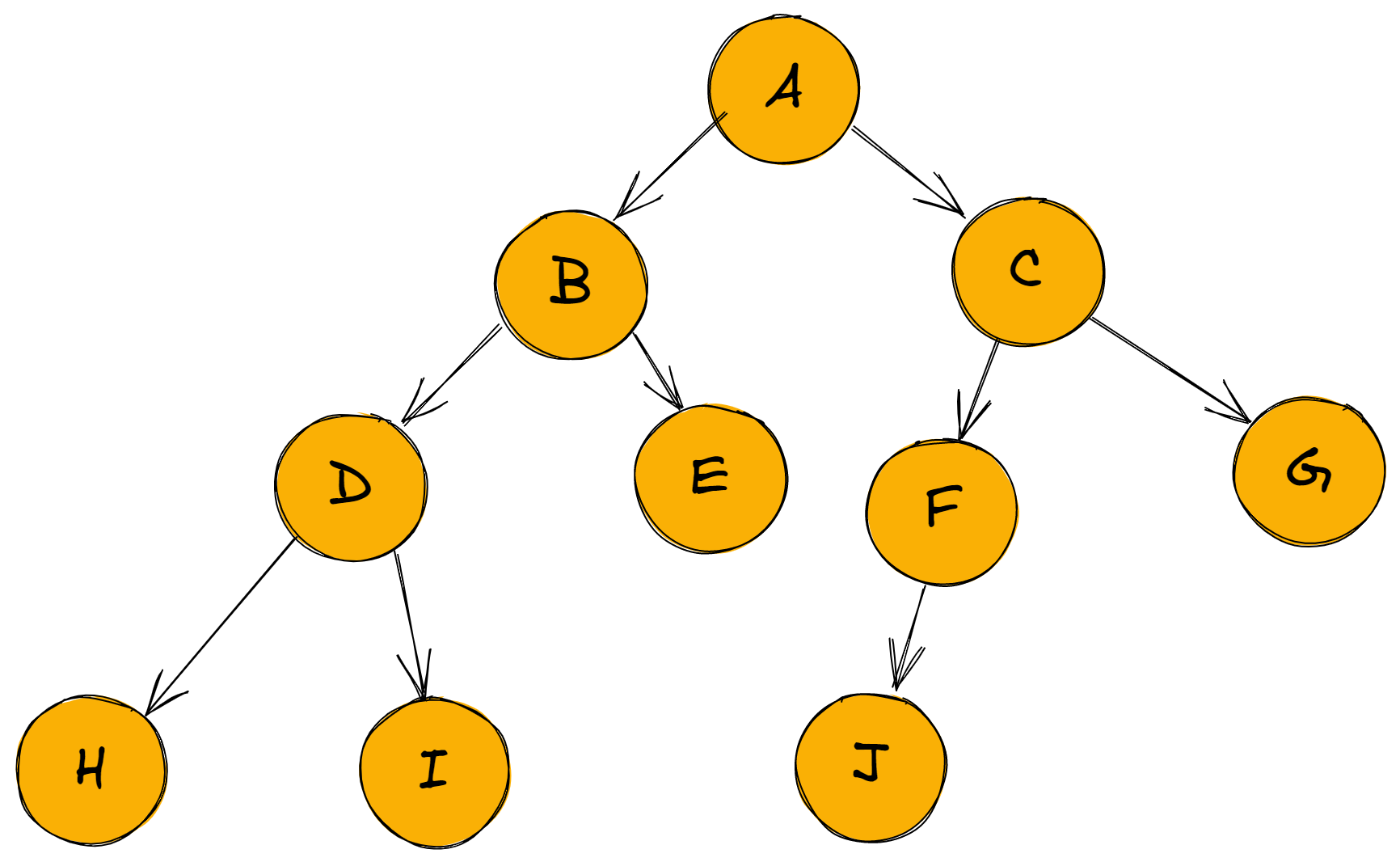
• 对于以上二叉树的创建可以直接通过节点之间的连接实现
• 此外我们还可以通过数组储存转为链式。

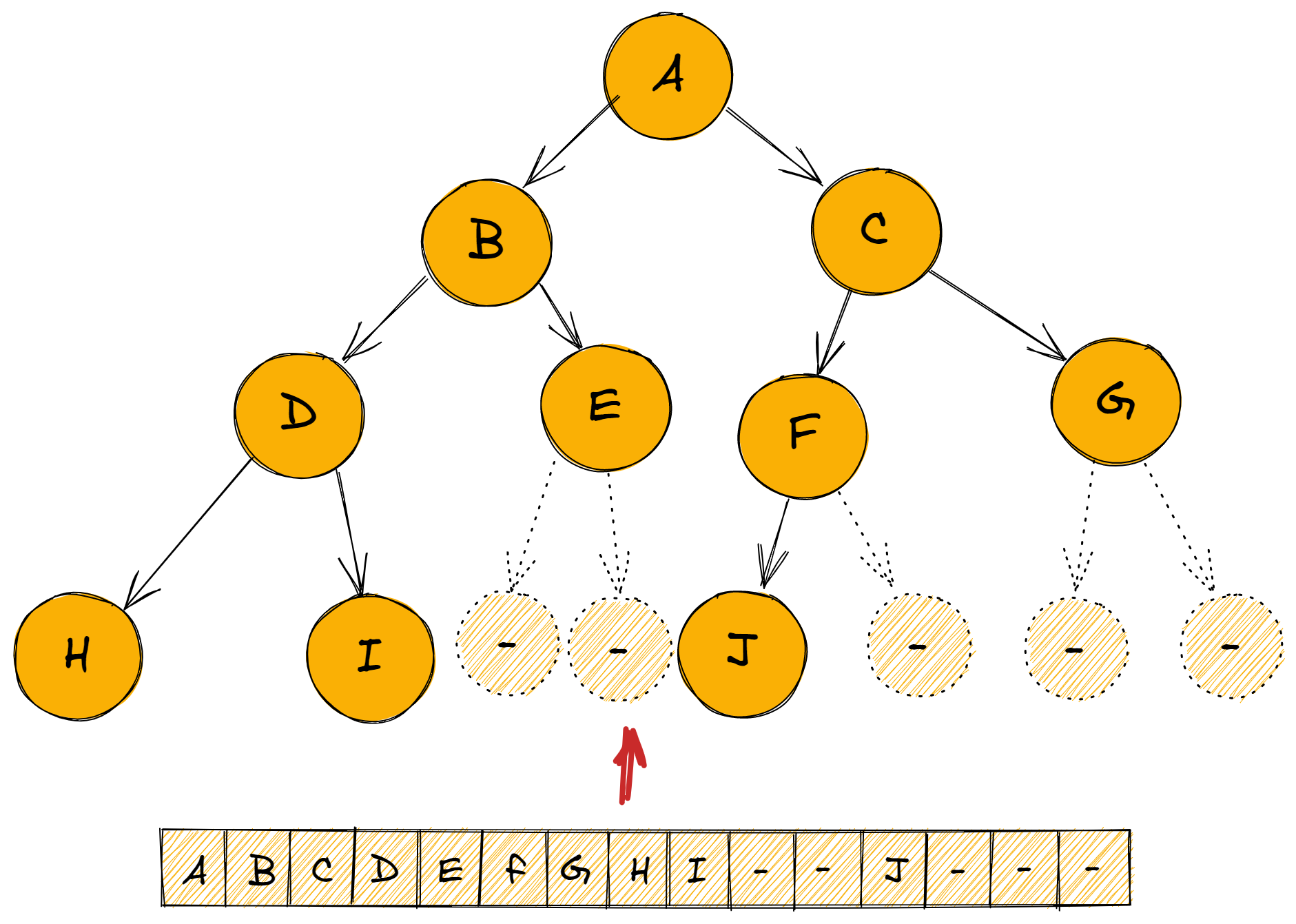
Go 语言代码参考

package main
​
import "fmt"
​
// 二叉树结构体
type bt struct {
    Val   string
    Left  *bt
    Right *bt
}
​
// 数组建立链式二叉树递归实现
func CreateTree(dataLst []string, i int) *bt {
    node := &bt{dataLst[i], nil, nil}
    if 2*i < len(dataLst) && dataLst[2*i] != "-" {
        node.Left = CreateTree(dataLst, 2*i)
    }
    if 2*i+1 < len(dataLst) && dataLst[2*i+1] != "-" {
        node.Right = CreateTree(dataLst, 2*i+1)
    }
    return node
}
​
// 数组建立链式二叉树非递归实现
func CreateTree_(dataLst []string) *bt {
    n := len(dataLst)
    nodeLst := make([]*bt, n)
    // 创建二叉树节点指针数组
    for i := 1; i < n; i++ {
        if dataLst[i] != "-" {
            nodeLst[i] = &bt{dataLst[i], nil, nil}
        }
    }
    // 连接二叉树左右节点
    for i := 1; i < n; i++ {
        if 2*i+1 < n {
            nodeLst[i].Left = nodeLst[2*i]
            nodeLst[i].Right = nodeLst[2*i+1]
        }
    }
    return nodeLst[1]
}
​
// 前序遍历
func preOrder(root *bt) {
    if root != nil {
        fmt.Print(root.Val, " ")
        preOrder(root.Left)
        preOrder(root.Right)
    }
}
​
// 中序遍历
func inOrder(root *bt) {
    if root != nil {
        inOrder(root.Left)
        fmt.Print(root.Val, " ")
        inOrder(root.Right)
    }
}
​
// 后序遍历
func posOrder(root *bt) {
    if root != nil {
        posOrder(root.Left)
        posOrder(root.Right)
        fmt.Print(root.Val, " ")
    }
}
​
func main() {
    // 直接创建二叉树
    root := &bt{
        "A",
        &bt{"B", &bt{"D", &bt{"H", nil, nil}, &bt{"I", nil, nil}}, &bt{"E", nil, nil}},
        &bt{"C", &bt{"F", &bt{"J", nil, nil}, nil}, &bt{"G", nil, nil}},
    }
    preOrder(root) // A B D H I E C F J G
    fmt.Println()
    inOrder(root) // H D I B E A J F C G
    fmt.Println()
    posOrder(root) // H I D E B J F G C A
    fmt.Println()
    fmt.Println("-------------------")
    // 数组非递归创建二叉树
    dl := []string{"-", "A", "B", "C", "D", "E", "F", "G", "H", "I", "-", "-", "J", "-", "-", "-"}
    root_ := CreateTree(dl, 1)
    preOrder(root_) // A B D H I E C F J G
    fmt.Println()
    inOrder(root_) // H D I B E A J F C G
    fmt.Println()
    posOrder(root_) // H I D E B J F G C A
    fmt.Println()
    fmt.Println("-------------------")
    root__ := CreateTree_(dl)
    preOrder(root__) // A B D H I E C F J G
    fmt.Println()
    inOrder(root__) // H D I B E A J F C G
    fmt.Println()
    posOrder(root__) // H I D E B J F G C A
}