2022年电工杯数模竞赛B题第一问解法分享（附 Python 代码）

Posted on | In ,

原文地址 zhuanlan.zhihu.com

题目

我们这里只分析第一问

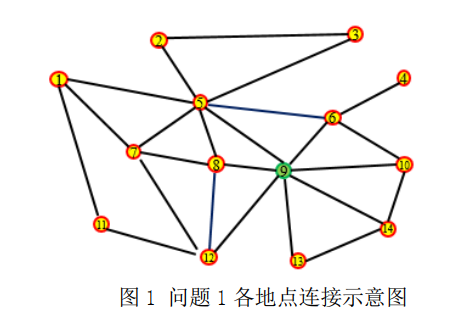
  1. 图 1 给出 14 个地点， 其中实线代表各地点之间的路线情况。 若目前所有应急物资集中在第 9 个地点，配送车辆的最大载重量为 1000 千克，采取配送车辆（无人机不参与）的配送模式。请结合附件 1， 建立完成一次整体配送的数学模型， 并给出最优方案。
    完成一次整体配送所需要的时间是按照配送车辆从出发开始至全部返回到出发地点的时间来计算。

附件 1：

邻接矩阵

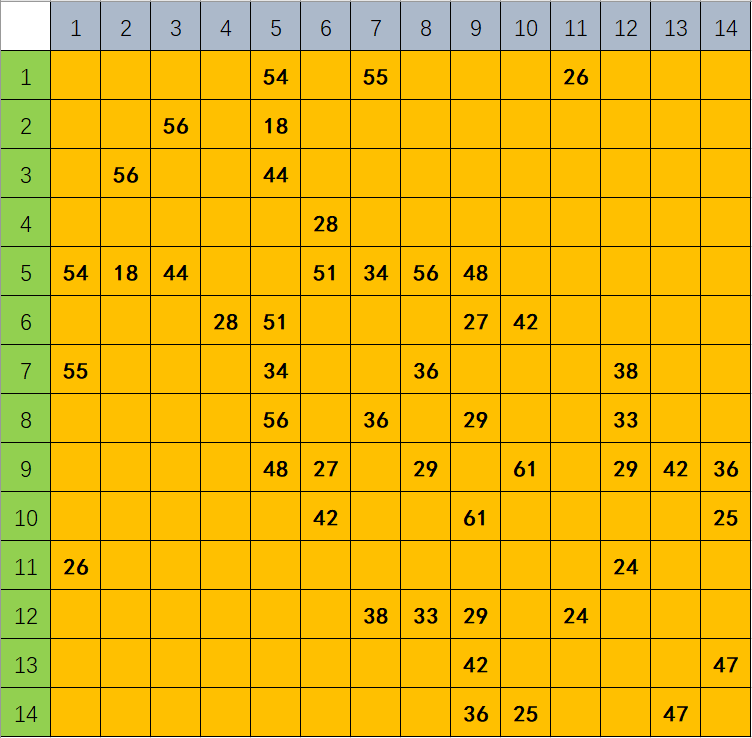
每个地点的需求量

题目分析

  • 所有地点的物资需求为 762kg，小于车辆的最大载重量 1000kg。也就是不需要车辆中途回去再取物资。
  • 整个物资配送路径最终得是个回路。
  • 由于给了个图，所以需要我们事先用图论相关算法求出任意两结点之间的最短路径。可以考虑迪杰斯特拉算法、弗洛伊德算法等。
  • 得到任意两点的最短路径矩阵（二维数组）后，我们就可以规划路线了。
  • 其实我们只要确定所有地点的访问顺序即可获得的具体的路线
  • 所有地点的访问顺序其实是一个全排列问题，即所有可能是： $1 \times 13 \times 12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \times 1=6,227,020,800$ 种访问顺序。其中第一个地点和最后一个地点的编号确定的。
  • 但是暴力枚举是 10 亿的数量级，需要很久可能几十个小时。
  • 所以我们要对枚举范围进行优化，即排除一些没必要的枚举。其实对于任意一个结点我们只需枚举最近的几个结点就可以了。比如：枚举最近的 4 个结点，原来有 13 个结点可以选择，现在我们只要枚举 4 结点就可以了。

首先，我们使用多次迪杰斯特拉算法得到了任意两节点之间的最短路径，然在在此基础上做访问顺序规划。我们以下的建模求解思路就是在暴力枚举的基础上做了剪枝优化，只枚举最近的 4 个结点的路线。当然，我们是有可能漏掉最佳答案的，但是一般情况下，这种可能性很小很小，所以我们是可以得到全局最优解的。

结果展示

最短距离矩阵

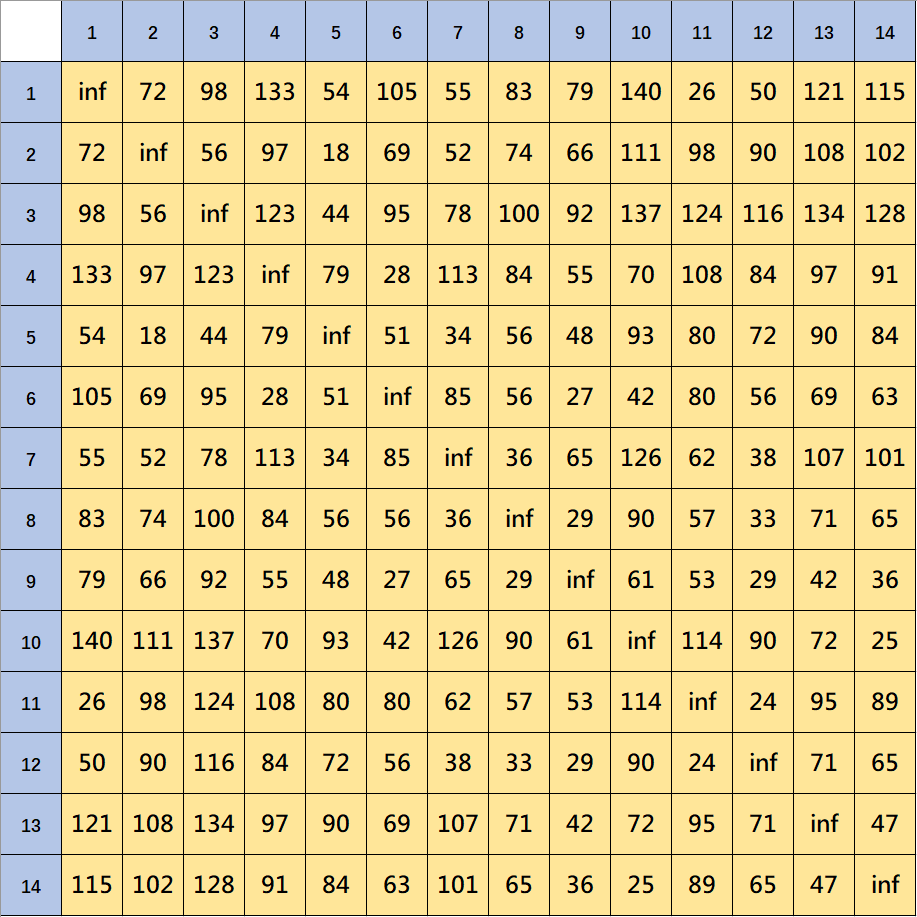
地点配送顺序

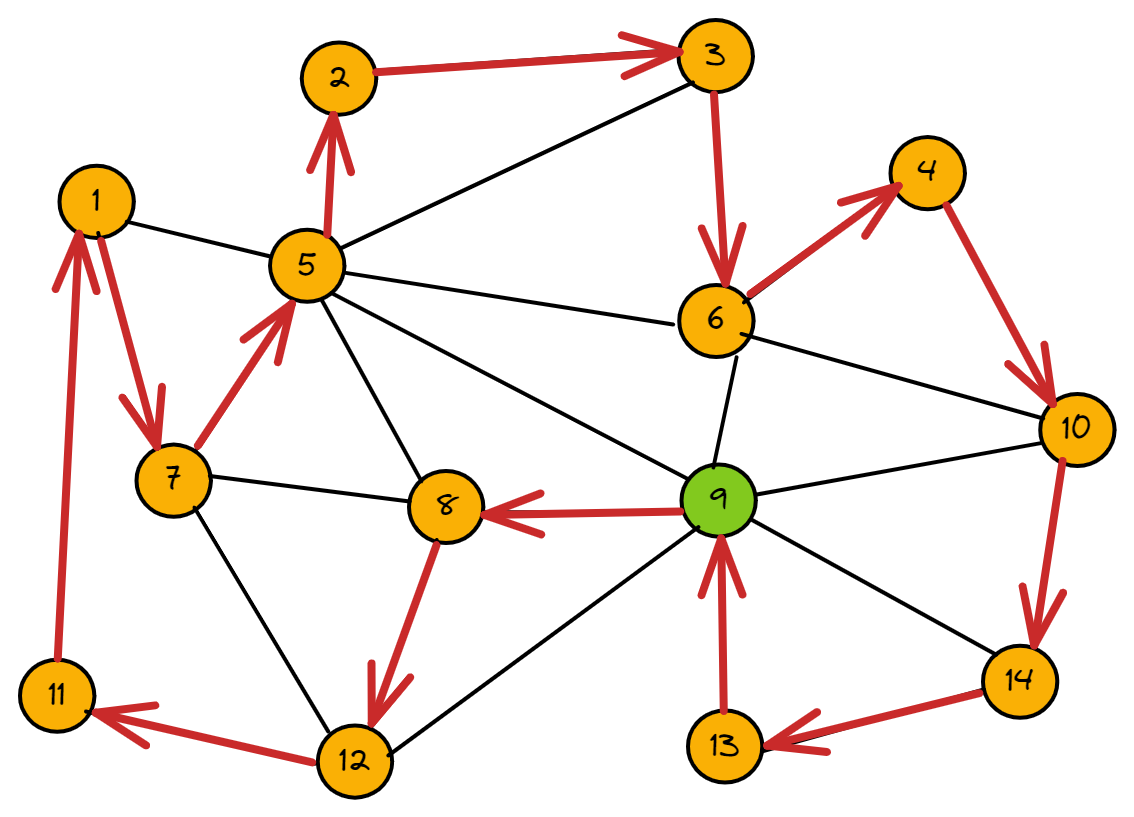
具体路线

$$
9 \rightarrow 8 \rightarrow 12 \rightarrow 11 \rightarrow 1 \rightarrow 7 \rightarrow 5 \rightarrow 2 \rightarrow 3 \rightarrow 5 \rightarrow 6 \rightarrow 4 \rightarrow 6 \rightarrow 10 \rightarrow 14 \rightarrow 13 \rightarrow 9
$$

总距离：582km

总耗时：11.64h

Python 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
from cmath import inf
from operator import truediv
​
print("--------------------------读取邻接矩阵---------------------------------")
'''
# 读取邻接矩阵
graph = []  # 保存邻接矩阵
with open("data.csv") as f:
    con = list(f.readlines())
    for line in con:
        line = line.split(',')
        line[-1] = line[-1][:-1]
        graph.append([int(i) if i != '' else inf for i in line])
​
n = len(graph)  # 地点个数
​
for i in range(n):  # 输出邻接矩阵
    print(graph[i])
​
'''
# 如果没有事先处理好本地文件直接用代码写入邻接矩阵也可
graph = [
    [inf , inf , inf , inf , 54  , inf , 55  , inf , inf , inf , 26  , inf , inf , inf ],
    [inf , inf , 56  , inf , 18  , inf , inf , inf , inf , inf , inf , inf , inf , inf ],
    [inf , 56  , inf , inf , 44  , inf , inf , inf , inf , inf , inf , inf , inf , inf ],
    [inf , inf , inf , inf , inf , 28  , inf , inf , inf , inf , inf , inf , inf , inf ],
    [54  , 18  , 44  , inf , inf , 51  , 34  , 56  , 48  , inf , inf , inf , inf , inf ],
    [inf , inf , inf , 28  , 51  , inf , inf , inf , 27  , 42  , inf , inf , inf , inf ],
    [55  , inf , inf , inf , 34  , inf , inf , 36  , inf , inf , inf , 38  , inf , inf ],
    [inf , inf , inf , inf , 56  , inf , 36  , inf , 29  , inf , inf , 33  , inf , inf ],
    [inf , inf , inf , inf , 48  , 27  , inf , 29  , inf , 61  , inf , 29  , 42  , 36  ],
    [inf , inf , inf , inf , inf , 42  , inf , inf , 61  , inf , inf , inf , inf , 25  ],
    [26  , inf , inf , inf , inf , inf , inf , inf , inf , inf , inf , 24  , inf , inf ],
    [inf , inf , inf , inf , inf , inf , 38  , 33  , 29  , inf , 24  , inf , inf , inf ],
    [inf , inf , inf , inf , inf , inf , inf , inf , 42  , inf , inf , inf , inf , 47  ],
    [inf , inf , inf , inf , inf , inf , inf , inf , 36  , 25  , inf , inf , 47  , inf ]
]

n = len(graph)  # 地点个数
​
print("-------------------------迪杰斯特拉算法----------------------------------")
# 迪杰斯特拉算法
def Dijkstra(s):
    vis = [False for i in range(n)]
    vis[s] = True
    for i in range(n):
        u = -1
        MIN = inf
        for j in range(n):
            if not vis[j] and MIN > graph[s][j]:
                u = j
                MIN = graph[s][j]
        if u == -1:
            return
        vis[u] = True
        for j in range(n):
            if not vis[j] and graph[u][j] != inf and graph[s][j] > graph[s][u]+graph[u][j]:
                graph[s][j] = graph[s][u] + graph[u][j]
​
for i in range(n):  # 多次迪杰斯特拉得到任意两点的最短路径
    Dijkstra(i)
​
for i in range(n):
    print(graph[i])
​
print("-------------------------最短路径----------------------------------")
# 最小路径回路模型
class MinLoop:
    '''
    该模型的使用前提是已经用算法整理了任意两点的最短路径的临界矩阵。
    我们这里使用的是用多次迪杰斯特拉算法得到的邻接矩阵
    '''
    def __init__(self,gp_min_dis,min_num,begin):
        '''
        gp_min_dis : List[List[float]] 或者 numpy二维数组 ---> 记录了图的任意两结点最短路径的邻接矩阵
        min_num : int ---> 枚举最近的结点路径数目
        begin : int ---> 路径的起始结点的下标
        '''
        self.gp_min_dis = gp_min_dis
        self.num = len(gp_min_dis)
        self.min_num = min_num
        self.begin = begin
        self.allPath = []       # 记录当前模型的所有可能路径
        self.allDistance = []   # 记录当前模型的所有可能路径的最短路径
        self.min_dis_dict = {}  # 将任意两点最短路径备份为字典以免修改原始数据
        for i in range(self.num):
            self.min_dis_dict[i] = gp_min_dis[i]
    
    # 获取当前模型的所有可能路径
    def genAllPath(self):
        path = [-1 for _ in range(self.num+1)]
        path[0] = self.begin
        path[-1] = self.begin
        self.DFS(0,self.begin,path)
        return self.allPath.copy()
​
    # 深度优先路径搜索
    def DFS(self,deep,pos,path):
        if deep == self.num-1:
            self.allPath.append(path.copy())
            return
​
        select = self.getSelect(path,pos)
        for nextPos in select:
            path[deep+1] = nextPos
            self.DFS(deep+1,nextPos,path)
            path[deep+1] = -1
​
    # 获取结点的未访问的最近几个结点
    def getSelect(self,path,pos):
        have = []
        for _ in range(self.min_num):
            min_dis_pos = -1
            min_dis = inf
            for j in range(self.num):
                if j not in path and j not in have:
                    if min_dis > self.min_dis_dict[pos][j]:
                        min_dis = self.min_dis_dict[pos][j]
                        min_dis_pos = j
            if min_dis_pos != -1:
                have.append(min_dis_pos)
        return have
    
    # 计算路径
    def getPathDistance(self,path):
        now = self.begin
        dis_sum = 0
        for to in path[1:]:
            dis_sum += self.min_dis_dict[now][to]
            now = to
        return dis_sum
    
    # 获取当前模型下的所有路径值
    def getAlldistance(self):
        distance_list = []
        for path in self.allPath:
            distance_list.append(self.getPathDistance(path))
        self.allDistance = distance_list
        return distance_list
​
    # 获取该模型的最短路径规划及路径值
    def getBestPath(self):
        bestDis = min(self.allDistance)
        for i in range(len(self.allDistance)):
            if bestDis == self.allDistance[i]:
                return (self.allPath[i].copy(),bestDis)
        return
​
model = MinLoop(graph,3,8)  # 选取最近的3个点进行枚举搜索
# 运行模型
model.genAllPath()
model.getAlldistance()
path,dis = model.getBestPath()
​
for i in range(len(path)):
    path[i] += 1    # 将下标改为标号
​
print("当前模型最短路径规划:",path) # [9, 8, 12, 11, 1, 7, 5, 2, 3, 6, 4, 10, 14, 13, 9]
print("当前模型最短路径值:",dis)   # 582.0
print("当前模型最短路径值耗时:",dis/50)   # 11.64