原文地址 zhuanlan.zhihu.com
Wallis公式是通过一个无穷积表达式计算$\pi$的方法
$$
\begin{align}
\frac{\pi}{2} &= \prod_{n=1}^\infty \frac{4 n^2}{4n^2 - 1} = \prod_{n=1}^\infty (\frac{2n}{2n + 1} \cdot \frac{2n}{2n - 1}) \
&= (\frac{2}{1} \cdot \frac{2}{3})\cdot(\frac{4}{3} \cdot \frac{4}{5})\cdot(\frac{6}{5}\cdot\frac{6}{7})(\frac{8}{7}\cdot\frac{8}{9})\cdot \cdots
\end{align}
$$
或者
$$
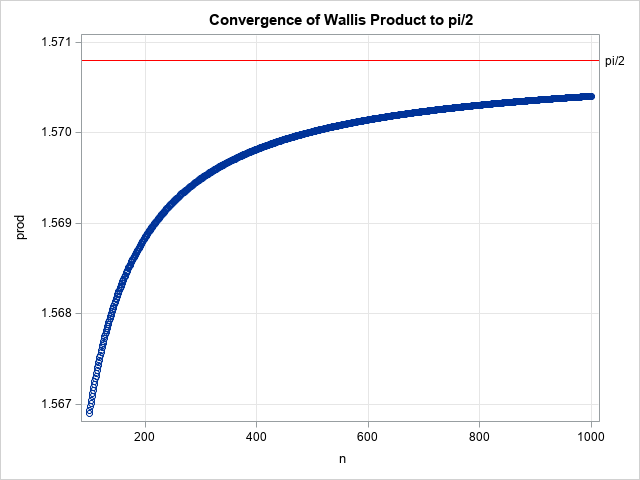
\lim_{n \to \infty} \frac{1}{2n + 1}[\frac{(2n)!!}{(2n - 1)!!}]^2 = \frac{\pi}{2}
$$
证明:
设 $I(n) = \int_0^{\frac{\pi}{2}} \sin^nx dx$
部分积分法拆分
$= \int_0^{\frac{\pi}{2}} \sin^{n - 1} x d (-\cos{x})$
$= \left.(-\cos x \sin^{n-1} x)\right|_0^{\frac{\pi}{2}} - \int_0^{\frac{\pi}{2}}(-\cos x)d \sin^{n-1} x$
$= \left.(-\cos x \sin^{n-1} x)\right|_0^{\frac{\pi}{2}} - \int_0^{\frac{\pi}{2}}(-\cos^2 x)(n - 1)\sin^{n-2} x dx$
$= (n - 1) \int_0^{\frac{\pi}{2}} \cos^2x \sin^{n-2}x dx$
$= (n - 1) \int_0^{\frac{\pi}{2}} (1 - \sin^2 x) \sin^{n-2}x dx$
$= (n - 1) \int_0^{\frac{\pi}{2}} (\sin^{n-2}x - \sin^n x) dx$
$= (n - 1) \int_0^{\frac{\pi}{2}} \sin^{n-2}x dx - (n - 1)\int_0^{\frac{\pi}{2}} \sin^n x dx$
$= (n - 1) I(n - 2) - (n - 1)I(n)$
$\Rightarrow I(n) = \frac{n - 1}{n} I (n - 2) \Rightarrow \begin{cases} \frac{I(2n + 1)} {I(2n - 1)} = \frac{2n}{2n + 1} \ \frac{I(2n)}{I(2n - 2)} = \frac{2n - 1}{2n} \end{cases}$
$\frac{I(3)}{I(1)} \cdot \frac{I(5)}{I(3)} \cdots \frac{I(2n + 1)}{I(2n - 1)} = \frac{2 \times 1}{2 \times 1 + 1} \times \frac{2 \times 2}{2 \times 2 + 1} \times \cdots \times \frac{2 n}{2n + 1} = \frac{(2n)!!}{(2n + 1)!!}$
$\frac{I(2)}{I(0)} \cdot \frac{I(4)}{I(2)} \cdots \frac{I(2n)}{I(2n - 2)} = \frac{2 \times 1 - 1}{2 \times 1} \times \frac{2 \times 2 - 1}{2 \times 2} \times \cdots \times \frac{2 n - 1}{2n} = \frac{(2n - 1)!!}{(2n)!!}$
左边的式子累称相消,最终得
$$
I(n) = \int_0^{\frac{\pi}{2}} \sin^n x dx = \begin{cases} \frac{\pi}{2} & n = 0 \ 1 & n =1 \ \frac{(2k)!!}{(2k + 1)!!} & n = 2k+1 \ \frac{(2k - 1)!!}{(2k)!!}\frac{\pi}{2} & n = 2k \end{cases}
$$
由 $\sin x$ 的单调性可知
$\sin^{2k + 1}x \leq \sin^{2k}x \leq \sin^{2k - 1}x,x\in [0,\frac{\pi}{2}]$
$\Downarrow$ 同时取定积分
$I(2k+1) < I(2k) < I(2k - 1)$
即得到
$\frac{(2k)!!}{(2k + 1)!!} < \frac{(2k - 1)!!}{(2k)!!} \frac{\pi}{2} < \frac{(2k - 2)!!}{(2k - 1)!!}$
$\frac{1}{2k+1} \cdot [\frac{(2k)!!}{(2k - 1)!!}]^2 < \frac{\pi}{2} < \frac{1}{2k} \cdot [\frac{(2k)!!}{(2k - 1)!!}]^2$
由夹逼定理可得
$\lim_{k \to \infty} \frac{1}{2k+1} \cdot [\frac{(2k)!!}{(2k - 1)!!}]^2 = \frac{\pi}{2}$