Posted on | In ,

原文地址 zhuanlan.zhihu.com

解氢原子薛定谔方程

薛定谔方程
$$
\left(-\frac{h^{2}}{8 \pi^{2} m_{e}} \nabla^{2}-\frac{Z e^{2}}{4 \pi \varepsilon_{0} r}\right) \psi=E \psi
$$
坐标轴转换
$$
\begin{cases}
x=r \sin \theta \cos \varphi \
y=r \sin \theta \sin \varphi \
z=r \cos \theta
\end{cases}
$$

$$
\begin{cases}
r^{2}=x^{2}+y^{2}+z^{2} \
\cos \theta=\frac{z}{\left(x^{2}+y^{2}+z^{2}\right)^{\frac{1}{2}}} \
\tan \varphi=\frac{y}{x}
\end{cases}
$$

拉普拉斯方程球坐标表示
$$
\nabla^{2}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2}}{\partial \varphi^{2}}
$$
球坐标下的薛定谔方程
$$
\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial \psi}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial \psi}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2} \psi}{\partial \varphi^{2}}+\frac{8 \pi^{2} m}{h^{2}}\left(E+\frac{Z e^{2}}{4 \pi \varepsilon_{0} r}\right) \psi=0
$$
通过解薛定谔方程（解法略过）可得氢原子的定态波函数：
$$
\Psi(r, \theta, \phi)=c\left[\sum_{I=1}^{n-1} c_{i}\left(\frac{Z r}{a_{0}}\right)^{l+i-1} e^{-\frac{Z_{r}}{n a_{0}}}\right] P_{l}^{|m|}(\cos \theta) e^{i m \phi}
$$

$n$为主量子数，取值为$1,2,3,…$

$l$为角量子数，取值为$0,1,2,…,n-1$

$m$为磁量子数，取值为$-l,-l+1,…,0,…,l-1,l$

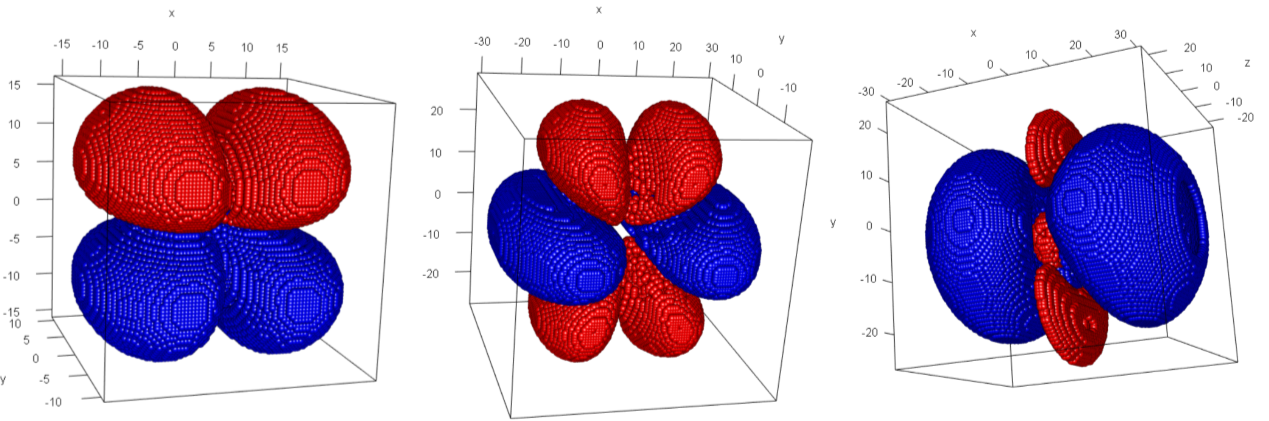
R 语言绘制波函数三维散点图

R 语言中可以绘制三维图像的包很多：plot3D,plotly,rgl,threejs等

目前小编还没有找到 R 语言直接绘制波函数原子轨道轮廓图的方法。这里我只展示绘制散点图来展示原子轨道的大致轮廓。

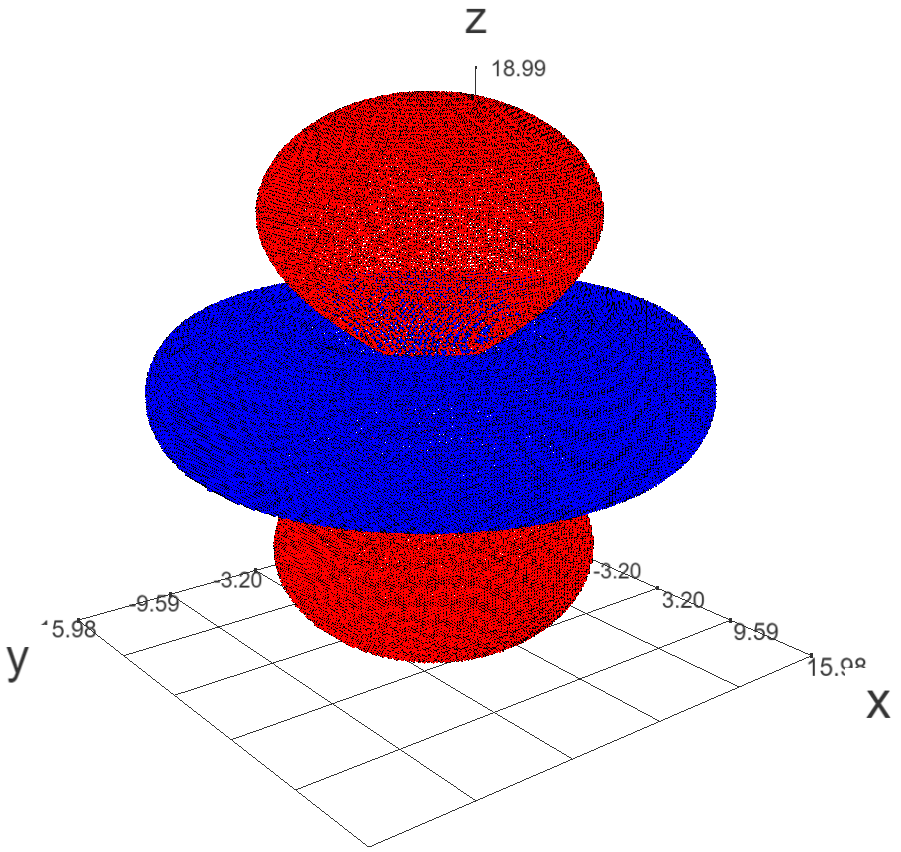
我们来绘制一下氢原子的$3d_{z^2}$轨道，波函数省去常数为：
$$
\psi = r^2 e^{-r/3} (3 \cos^2 \theta - 1)
$$

我的绘制思路就是在一个三维正方体域内计算波函数值，再求解得到的波函数值平方的平均值。然后绘制平均值上下范围内的散点即可。这里我用rgl包的plot3D函数做演示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
library(rgl)
​
# 定义波函数
wavefunction <- function(r,theta,phi) r^2*exp(-r/3)*(3*cos(theta)^2-1)
​
# 设定超参，m不应小于20否则绘制图像不完整
num <- 100  # 反映散点密度
m <- 20 # 范围
​
# 初始化一个正方体域
xt <- rep(seq(-m,m,length = num),each = num^2)
yt <- rep(rep(seq(-m,m,length = num),each = num),num)
zt <- rep(seq(-m,m,length = num),num^2)
​
# 转为球坐标参数
r <- sqrt(xt^2+yt^2+zt^2)
theta <- acos(zt/r)
phi <- atan(yt/xt)
​
# 计算波函数
wv <- wavefunction(r,theta,phi)
​
mn <- mean(wv^2,na.rm = T)  # 波函数平方的平均值
drw <- !is.na(wv)&wv^2<mn&wv^2>0.8*mn   # 找出波函数平方平均值0.8~1倍的点集
​
cl <- ifelse(wv>0,"red","blue") # 波函数为正的用红色标注，负的用蓝色
cl <- cl[drw]
​
# 找出满足波函数的x,y,z坐标
x <- xt[drw]
y <- yt[drw]
z <- zt[drw]
​
# 绘制三维散点图
plot3d(x,y,z,size = 1,type = "s",col = cl,alpha = 0.1)

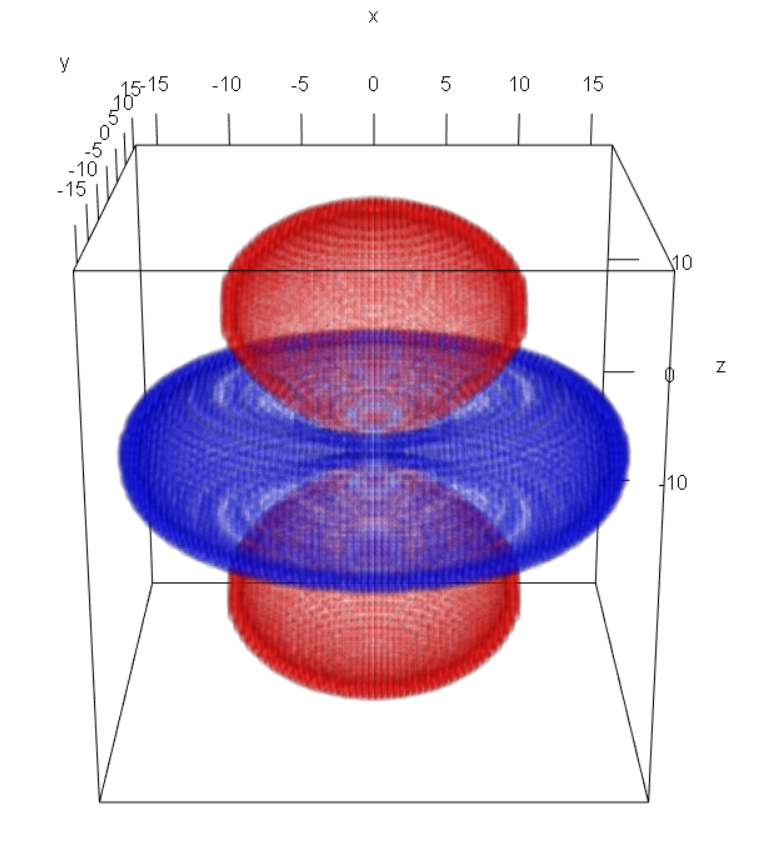
此外我们可以试试其他包函数绘制

1
2
3
library(threejs)
scatterplot3js(x, y, z, color =  cl, size = 0.1)

1
2
3
4
# 还可以尝试使用其他相关的3D绘图包进行绘制
library(plotly)
library(plot3D)

示例展示

Posted on | In ,

原文地址 zhuanlan.zhihu.com

生成数据

  • 生成线性相关的散点数据
1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
import matplotlib.pyplot as plt
​
num = 20    # 散点数目
​
# 数据生成
px = np.arange(num)
py = 2*px-4+5*np.random.random(num) # 加上噪声
​
# 散点图
plt.scatter(px,py)
plt.show()

线性回归模型

$$
y = kx + b
$$

我们需要找到一个合适的参数k和b模型的预测值与真实值差异最小化。

预测值与真实值差异使用均方误差来体现：
$$
L(k,b) = \frac{1}{2n} \sum_{i=1}^{n} (\hat y_i - y_i)^2 = \frac{1}{2n} \sum_{i=1}^{n} (k x_i + b - y_i)^2
$$
其中$\hat y$是预测值，$y$是真实值。直观的来看，就是所有预测点到真实点的距离平均值的一半。这个式子我们也叫做损失函数。

梯度下降法

为了得到总误差最小的线性模型，我们将使用梯度下降法。

梯度下降法的迭代关系式：
$$
\begin{align}
k_i &= k_{i-1} - \alpha \cdot \frac{\partial L}{\partial k_{i-1}} \
b_i &= b_{i-1} - \alpha \cdot \frac{\partial L}{\partial b_{i-1}}
\end{align}
$$
其中$\alpha$是步长，也称学习率。这里的$k_0,b_0$我们可以随机初始化一个数字。

通过微积分公式我们可以计算得知：
$$
\begin{align}
\frac{\partial L}{\partial k} &= \frac{1}{n} \sum_{i=1}^{n} (k x_i + b - y_i) \cdot x_i \
\frac{\partial L}{\partial b} &= \frac{1}{n} \sum_{i=1}^{n} (k x_i + b - y_i)
\end{align}
$$

算法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
# 模型函数
def f(x,k,b):
    return k*x+b
​
# 损失函数
def L(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(len(x)):
        s += (k*x[i]+b-y[i])**2
    return s/2
​
# k梯度
def grad_k(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(n):
        s += (k*x[i]+b-y[i])*x[i]
    return s/n
​
# b梯度
def grad_b(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(n):
        s += (k*x[i]+b-y[i])
    return s/n
​
# 初始化参数
k = 0
b = 0
​
times = 100     # 训练次数
alpha = 0.01    # 步长
​
for i in range(times):
    # 梯度下降迭代
    k = k - alpha*grad_k(px,py,k,b)
    b = b - alpha*grad_b(px,py,k,b)
    if i%20 == 0:
        print("%d:%.2f"%(i,L(px,py,k,b)))   # 输出当前损失函数
​
plt.plot(px,f(px,k,b),c = "red")    # 绘制训练结果
plt.show()

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import numpy as np
import matplotlib.pyplot as plt
​
num = 20    # 散点数目
​
# --------------数据生成----------------
px = np.arange(num)
py = 2*px-4+5*np.random.random(num) # 加上噪声
​
# 散点图
plt.scatter(px,py)
# plt.show()
​
# --------------模型搭建-----------------
# 模型函数
def f(x,k,b):
    return k*x+b
​
# 损失函数
def L(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(len(x)):
        s += (k*x[i]+b-y[i])**2
    return s/2
​
# k梯度
def grad_k(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(n):
        s += (k*x[i]+b-y[i])*x[i]
    return s/n
​
# b梯度
def grad_b(x,y,k,b):
    s = 0
    n = len(x)
    for i in range(n):
        s += (k*x[i]+b-y[i])
    return s/n
​
# --------------梯度下降-----------------
# 初始化参数
k = 0
b = 0
​
times = 100     # 训练次数
alpha = 0.01    # 步长
​
for i in range(times):
    # 梯度下降迭代
    k = k - alpha*grad_k(px,py,k,b)
    b = b - alpha*grad_b(px,py,k,b)
    if i%20 == 0:
        print("%d:%.2f"%(i,L(px,py,k,b)))   # 输出当前损失函数
​
plt.plot(px,f(px,k,b),c = "red")    # 绘制训练结果
plt.show()

Posted on | In

原文地址 zhuanlan.zhihu.com

Minimax 算法即极小极大值算法，是一种回溯算法，用于决策制定和博弈论。尤其是在双人之间的零和博弈中，假定两人都是绝对理性的情况下找出最佳决策方式。他广泛应用于两人回合制游戏，例如井字棋，国际象棋等。

在 Minimax 中，两人被称为最大化者和最小化者。最大化者试图获得尽可能高的分数，而最小化者试图做相反的事情并获得尽可能低的分数。

每个棋盘状态都有一个与之关联的值。在给定的状态下，如果最大化者占上风，那么棋盘的得分将趋向于某个正值。如果最小化者在该棋盘状态下占上风，那么它往往是一些负值。棋盘的价值是通过一些启发式计算的，这些启发式对于每种类型的游戏都是独一无二的。

评价函数

1
2
3
4
5
func evaluate(board [][]byte) int {
    var score int
    // 计算得失
    return score
}

对于双人零和博弈游戏来说，我必须首先制定一套根据实际状态计算双方得失的函数，我们称其为评价函数。 拿棋类游戏来举例的话，就是根据当前的棋盘状态 board 制定一套计算双方得失的规则，然后计算分数 score 返回。

minimax 函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func minimax(board [][]byte,depth int,isMax bool) int {
    /*
    board是当前棋盘状态
    depth当前递归深度
    isMax是回合布尔值
    */
    // 边界条件
    if /*终端状态*/ {
        return /*当前状态下的评价分数值*/
    }
    
    // 决策树的遍历
    if isMax {
        // 最大化者的最大化评价分数的选择
        score := -INFINITY
        for /*当前回合的所有状态*/ {
            // 状态假定选择
            // 选择撤销
        }
        return score
    } else {
        // 最小化者的最小化评价分数的选择
        score := +INFINITY
        for /*当前回合的所有状态*/ {
            // 状态假定选择
            // 选择撤销
        }
        return score
    }
}

max 最大化者代表我方，min 最小化者代表对手。我方要尽可能令评价分数最大化，对方要尽可能令评价分数最小化。

这个函数实质上就是对决策树进行遍历，返回对我方最有利，即评价分数最高的值。

最佳走法函数

1
2
3
4
5
6
7
8
9
10
11
// 决策（棋法）结构体
type Move struct {
    Position int
    ...
}
​
func findBestMove(board [][]byte) Move {
    var bestMove Move
    // 遍历当前回合的所有决策，寻找最大值
    return bestMove
}

利用 minima 函数返回最佳决策（走法）。

数学原理

$$
v_i = \mathop{max}\limits_{a_i} \ \mathop{min}\limits_{a_{-i}} \ v_i(a_i,a_{-i})
$$

$i$ 是当前玩家索引
$-i$ 是对手玩家索引
$a_i$ 代表当前玩家采取的行动
$a_{-i}$ 代表对手玩家采取的行动
$v_i$ 是当前局势状态的评估价值

$v_i$ 越是大的正数代表当前局势对于玩家 $i$ 更有利，$v_i$ 越是小的的负数代表当前局势对于玩家 $-i$ 更有利

minimax 算法伪代码

1
2
3
4
5
6
7
8
9
10
11
12
13
function  minimax(node, depth, maximizingPlayer) is
    if depth = 0 or node is a terminal node then
        return the heuristic value of node
    if maximizingPlayer then
        value := −∞
        for each child of node do
            value := max(value, minimax(child, depth − 1, FALSE))
        return value
    else (* minimizing player *)
        value := +∞
        for each child of node do
            value := min(value, minimax(child, depth − 1, TRUE))
        return value

图解算法：实际上就是决策树的遍历过程

实例代码 - Go 语言

minimax 算法游戏 AI

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
package main
​
import "fmt"
​
// 走法结构体
type Move struct {
    row, col int
}
​
// 评价函数
func evaluate(board [3][3]byte) int {
    // Rows
    for row := 0; row < 3; row++ {
        if board[row][0] == board[row][1] && board[row][1] == board[row][2] {
            if board[row][0] == 'x' {
                return 1
            }
            if board[row][0] == 'o' {
                return -1
            }
        }
    }
    // Colums
    for col := 0; col < 3; col++ {
        if board[0][col] == board[1][col] && board[1][col] == board[2][col] {
            if board[0][col] == 'x' {
                return 1
            }
            if board[0][col] == 'o' {
                return -1
            }
        }
    }
    // Diagonals
    if board[0][0] == board[1][1] && board[1][1] == board[2][2] {
        if board[0][0] == 'x' {
            return 1
        }
        if board[0][0] == 'o' {
            return -1
        }
    }
    if board[0][2] == board[1][1] && board[1][1] == board[2][0] {
        if board[0][2] == 'x' {
            return 1
        }
        if board[0][2] == 'o' {
            return -1
        }
    }
    return 0
}
​
// minimax函数
func minimax(board [3][3]byte, isMax bool) int {
    score := evaluate(board)
    if score != 0 {
        return score
    }
    if isFull(board) {
        return 0
    }
​    // 回合判断
    if isMax {
        maxVal := -10
        for row := 0; row < 3; row++ {
            for col := 0; col < 3; col++ {
                if board[row][col] == '-' {
                    board[row][col] = 'x'
                    maxVal = max(maxVal, minimax(board, !isMax))
                    board[row][col] = '-'
                }
            }
        }
        return maxVal
    } else {
        minVal := 10
        for row := 0; row < 3; row++ {
            for col := 0; col < 3; col++ {
                if board[row][col] == '-' {
                    board[row][col] = 'o'
                    minVal = min(minVal, minimax(board, !isMax))
                    board[row][col] = '-'
                }
            }
        }
        return minVal
    }
}
​
// 最佳走法函数
func bestMove(board [3][3]byte) Move {
    var move Move
    move.row, move.col = -1, -1
    minVal := 10
    for row := 0; row < 3; row++ {
        for col := 0; col < 3; col++ {
            if board[row][col] == '-' {
                board[row][col] = 'o'
                moveVal := minimax(board, true)
                board[row][col] = '-'
                if moveVal < minVal {
                    move.row = row
                    move.col = col
                    minVal = moveVal
                }
            }
        }
    }
    fmt.Println()
    return move
}
​
// 判断是否棋盘已满
func isFull(board [3][3]byte) bool {
    for row := 0; row < 3; row++ {
        for col := 0; col < 3; col++ {
            if board[row][col] == '-' {
                return false
            }
        }
    }
    return true
}
​
func max(a, b int) int {
    if a > b {
        return a
    }
    return b
}
​
func min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

主程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
package main
​
import "fmt"
​
// 游戏状态结构体
type GameState struct {
    board [3][3]byte
}
​
// 判断是否为空棋格
func isEmpty(board [3][3]byte, row, col int) bool {
    if board[row][col] == '-' {
        return true
    }
    return false
}
​
// 判断是否获胜
func isWin(board [3][3]byte) bool {
    // Rows
    for row := 0; row < 3; row++ {
        if board[row][0] == board[row][1] && board[row][1] == board[row][2] && board[row][0] != '-' {
            return true
        }
    }
    // Colums
    for col := 0; col < 3; col++ {
        if board[0][col] == board[1][col] && board[1][col] == board[2][col] && board[0][col] != '-' {
            return true
        }
    }
    // Diagonals
    if board[0][0] == board[1][1] && board[1][1] == board[2][2] && board[0][0] != '-' {
        return true
    }
    if board[0][2] == board[1][1] && board[1][1] == board[2][0] && board[0][2] != '-' {
        return true
    }
    return false
}
​
// 判断是否游戏结束
func isEnd(board [3][3]byte) bool {
    if isWin(board) {
        return true
    }
    for row := 0; row < 3; row++ {
        for col := 0; col < 3; col++ {
            if isEmpty(board, row, col) {
                return false
            }
        }
    }
    return true
}
​
// 显示棋盘状态
func showBoard(board [3][3]byte) {
    for row := 0; row < 3; row++ {
        for col := 0; col < 3; col++ {
            fmt.Printf("%c ", board[row][col])
        }
        fmt.Println()
    }
}
​
func main() {
    var gs GameState
    gs.board = [3][3]byte{
        {'-', '-', '-'},
        {'-', '-', '-'},
        {'-', '-', '-'},
    }
    showBoard(gs.board)
    var row, col int
    for !isEnd(gs.board) {
        fmt.Scanf("%d %d", &row, &col)
        if isEmpty(gs.board, row, col) {
            gs.board[row][col] = 'x'
            showBoard(gs.board)
            fmt.Println()
            if isEnd(gs.board) {
                fmt.Println("Game Over")
                break
            }
            oMove := bestMove(gs.board)
            gs.board[oMove.row][oMove.col] = 'o'
            showBoard(gs.board)
            fmt.Println("-------------------------------------------------------------------------------------------")
        }
    }
}

控制台

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
- - - 
- - -
- - -
1 1
- - - 
- x -
- - -
​
o - -
- x -
- - -
-----------------------------------------------------------------------------------------------------------------------
2 0
o - - 
- x -
x - -

o - o
- x -
x - -
-----------------------------------------------------------------------------------------------------------------------
2 2
o - o 
- x -
x - x
​
o o o
- x -
x - x
-----------------------------------------------------------------------------------------------------------------------

Posted on | In ,

原文地址 zhuanlan.zhihu.com

题目

我们这里只分析第一问

  1. 图 1 给出 14 个地点， 其中实线代表各地点之间的路线情况。 若目前所有应急物资集中在第 9 个地点，配送车辆的最大载重量为 1000 千克，采取配送车辆（无人机不参与）的配送模式。请结合附件 1， 建立完成一次整体配送的数学模型， 并给出最优方案。
    完成一次整体配送所需要的时间是按照配送车辆从出发开始至全部返回到出发地点的时间来计算。

附件 1：

邻接矩阵

每个地点的需求量

题目分析

  • 所有地点的物资需求为 762kg，小于车辆的最大载重量 1000kg。也就是不需要车辆中途回去再取物资。
  • 整个物资配送路径最终得是个回路。
  • 由于给了个图，所以需要我们事先用图论相关算法求出任意两结点之间的最短路径。可以考虑迪杰斯特拉算法、弗洛伊德算法等。
  • 得到任意两点的最短路径矩阵（二维数组）后，我们就可以规划路线了。
  • 其实我们只要确定所有地点的访问顺序即可获得的具体的路线
  • 所有地点的访问顺序其实是一个全排列问题，即所有可能是： $1 \times 13 \times 12 \times 11 \times 10 \times 9 \times 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1 \times 1=6,227,020,800$ 种访问顺序。其中第一个地点和最后一个地点的编号确定的。
  • 但是暴力枚举是 10 亿的数量级，需要很久可能几十个小时。
  • 所以我们要对枚举范围进行优化，即排除一些没必要的枚举。其实对于任意一个结点我们只需枚举最近的几个结点就可以了。比如：枚举最近的 4 个结点，原来有 13 个结点可以选择，现在我们只要枚举 4 结点就可以了。

首先，我们使用多次迪杰斯特拉算法得到了任意两节点之间的最短路径，然在在此基础上做访问顺序规划。我们以下的建模求解思路就是在暴力枚举的基础上做了剪枝优化，只枚举最近的 4 个结点的路线。当然，我们是有可能漏掉最佳答案的，但是一般情况下，这种可能性很小很小，所以我们是可以得到全局最优解的。

结果展示

最短距离矩阵

地点配送顺序

具体路线

$$
9 \rightarrow 8 \rightarrow 12 \rightarrow 11 \rightarrow 1 \rightarrow 7 \rightarrow 5 \rightarrow 2 \rightarrow 3 \rightarrow 5 \rightarrow 6 \rightarrow 4 \rightarrow 6 \rightarrow 10 \rightarrow 14 \rightarrow 13 \rightarrow 9
$$

总距离：582km

总耗时：11.64h

Python 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
from cmath import inf
from operator import truediv
​
print("--------------------------读取邻接矩阵---------------------------------")
'''
# 读取邻接矩阵
graph = []  # 保存邻接矩阵
with open("data.csv") as f:
    con = list(f.readlines())
    for line in con:
        line = line.split(',')
        line[-1] = line[-1][:-1]
        graph.append([int(i) if i != '' else inf for i in line])
​
n = len(graph)  # 地点个数
​
for i in range(n):  # 输出邻接矩阵
    print(graph[i])
​
'''
# 如果没有事先处理好本地文件直接用代码写入邻接矩阵也可
graph = [
    [inf , inf , inf , inf , 54  , inf , 55  , inf , inf , inf , 26  , inf , inf , inf ],
    [inf , inf , 56  , inf , 18  , inf , inf , inf , inf , inf , inf , inf , inf , inf ],
    [inf , 56  , inf , inf , 44  , inf , inf , inf , inf , inf , inf , inf , inf , inf ],
    [inf , inf , inf , inf , inf , 28  , inf , inf , inf , inf , inf , inf , inf , inf ],
    [54  , 18  , 44  , inf , inf , 51  , 34  , 56  , 48  , inf , inf , inf , inf , inf ],
    [inf , inf , inf , 28  , 51  , inf , inf , inf , 27  , 42  , inf , inf , inf , inf ],
    [55  , inf , inf , inf , 34  , inf , inf , 36  , inf , inf , inf , 38  , inf , inf ],
    [inf , inf , inf , inf , 56  , inf , 36  , inf , 29  , inf , inf , 33  , inf , inf ],
    [inf , inf , inf , inf , 48  , 27  , inf , 29  , inf , 61  , inf , 29  , 42  , 36  ],
    [inf , inf , inf , inf , inf , 42  , inf , inf , 61  , inf , inf , inf , inf , 25  ],
    [26  , inf , inf , inf , inf , inf , inf , inf , inf , inf , inf , 24  , inf , inf ],
    [inf , inf , inf , inf , inf , inf , 38  , 33  , 29  , inf , 24  , inf , inf , inf ],
    [inf , inf , inf , inf , inf , inf , inf , inf , 42  , inf , inf , inf , inf , 47  ],
    [inf , inf , inf , inf , inf , inf , inf , inf , 36  , 25  , inf , inf , 47  , inf ]
]

n = len(graph)  # 地点个数
​
print("-------------------------迪杰斯特拉算法----------------------------------")
# 迪杰斯特拉算法
def Dijkstra(s):
    vis = [False for i in range(n)]
    vis[s] = True
    for i in range(n):
        u = -1
        MIN = inf
        for j in range(n):
            if not vis[j] and MIN > graph[s][j]:
                u = j
                MIN = graph[s][j]
        if u == -1:
            return
        vis[u] = True
        for j in range(n):
            if not vis[j] and graph[u][j] != inf and graph[s][j] > graph[s][u]+graph[u][j]:
                graph[s][j] = graph[s][u] + graph[u][j]
​
for i in range(n):  # 多次迪杰斯特拉得到任意两点的最短路径
    Dijkstra(i)
​
for i in range(n):
    print(graph[i])
​
print("-------------------------最短路径----------------------------------")
# 最小路径回路模型
class MinLoop:
    '''
    该模型的使用前提是已经用算法整理了任意两点的最短路径的临界矩阵。
    我们这里使用的是用多次迪杰斯特拉算法得到的邻接矩阵
    '''
    def __init__(self,gp_min_dis,min_num,begin):
        '''
        gp_min_dis : List[List[float]] 或者 numpy二维数组 ---> 记录了图的任意两结点最短路径的邻接矩阵
        min_num : int ---> 枚举最近的结点路径数目
        begin : int ---> 路径的起始结点的下标
        '''
        self.gp_min_dis = gp_min_dis
        self.num = len(gp_min_dis)
        self.min_num = min_num
        self.begin = begin
        self.allPath = []       # 记录当前模型的所有可能路径
        self.allDistance = []   # 记录当前模型的所有可能路径的最短路径
        self.min_dis_dict = {}  # 将任意两点最短路径备份为字典以免修改原始数据
        for i in range(self.num):
            self.min_dis_dict[i] = gp_min_dis[i]
    
    # 获取当前模型的所有可能路径
    def genAllPath(self):
        path = [-1 for _ in range(self.num+1)]
        path[0] = self.begin
        path[-1] = self.begin
        self.DFS(0,self.begin,path)
        return self.allPath.copy()
​
    # 深度优先路径搜索
    def DFS(self,deep,pos,path):
        if deep == self.num-1:
            self.allPath.append(path.copy())
            return
​
        select = self.getSelect(path,pos)
        for nextPos in select:
            path[deep+1] = nextPos
            self.DFS(deep+1,nextPos,path)
            path[deep+1] = -1
​
    # 获取结点的未访问的最近几个结点
    def getSelect(self,path,pos):
        have = []
        for _ in range(self.min_num):
            min_dis_pos = -1
            min_dis = inf
            for j in range(self.num):
                if j not in path and j not in have:
                    if min_dis > self.min_dis_dict[pos][j]:
                        min_dis = self.min_dis_dict[pos][j]
                        min_dis_pos = j
            if min_dis_pos != -1:
                have.append(min_dis_pos)
        return have
    
    # 计算路径
    def getPathDistance(self,path):
        now = self.begin
        dis_sum = 0
        for to in path[1:]:
            dis_sum += self.min_dis_dict[now][to]
            now = to
        return dis_sum
    
    # 获取当前模型下的所有路径值
    def getAlldistance(self):
        distance_list = []
        for path in self.allPath:
            distance_list.append(self.getPathDistance(path))
        self.allDistance = distance_list
        return distance_list
​
    # 获取该模型的最短路径规划及路径值
    def getBestPath(self):
        bestDis = min(self.allDistance)
        for i in range(len(self.allDistance)):
            if bestDis == self.allDistance[i]:
                return (self.allPath[i].copy(),bestDis)
        return
​
model = MinLoop(graph,3,8)  # 选取最近的3个点进行枚举搜索
# 运行模型
model.genAllPath()
model.getAlldistance()
path,dis = model.getBestPath()
​
for i in range(len(path)):
    path[i] += 1    # 将下标改为标号
​
print("当前模型最短路径规划:",path) # [9, 8, 12, 11, 1, 7, 5, 2, 3, 6, 4, 10, 14, 13, 9]
print("当前模型最短路径值:",dis)   # 582.0
print("当前模型最短路径值耗时:",dis/50)   # 11.64

Posted on | In

原文地址 zhuanlan.zhihu.com

琴生不等式

若 $f(x)$ 是区间 $[a,b]$ 上的下凸函数，则对任意的 $x_1,x_2,\dots,x_n \in [a,b]$，则有不等式:
$$
\frac{\sum_{i = 1}^n f(x_i)}{n} \geq f(\frac{\sum_{i = 1}^n x_i}{n})
$$
当且仅当 $x_1 = x_2 = x_3 = \dots = x_n$ 时等号成立

均值不等式

对于若干个非负数 $x_1,x_2,\dots,x_n$ 有不等式：
$$
\frac{\sum_{i = 1}^n x_i}{n} \geq \sqrt[n]{\prod_{i=1}^n x_i}
$$
当且仅当 $x_1 = x_2 = x_3 = \dots = x_n$ 时等号成立

证明：

设 $f(x) = -\ln x , x > 0$

$f’(x) = -\frac{1}{x} , f’’(x) = \frac{1}{x^2} > 0$

即 $f(x)$ 为下凸函数，应用琴生不等式可得

$\frac{f(x_1) + f(x_2) + \dots + f(x_n)}{n} \geq f(\frac{x_1 + x_2 + \dots + x_n}{n})$

$- \frac{\ln x_1 + \ln x_2 + \dots + \ln x_n}{n} \geq - \ln(\frac{x_1 + x_2 + \dots + x_n}{n})$

$\frac{\ln{(x_1 x_2 \dots x_n)}}{n} \leq \ln{(\frac{x_1 + x_2 + \dots + x_n}{n})}$

$\ln{(x_1 x_2 \dots x_n)^{\frac{1}{n}}} \leq \ln{(\frac{x_1 + x_2 + \dots + x_n}{n})}$

$(x_1 x_2 \dots x_n)^{\frac{1}{n}} \leq \frac{x_1 + x_2 + \dots + x_n}{n}$

则 $\frac{\sum_{i = 1}^n x_i}{n} \geq \sqrt[n]{\prod_{i=1}^n x_i}$

证毕